 por riickscrotzze » Ter Jun 04, 2013 15:55
por riickscrotzze » Ter Jun 04, 2013 15:55
Olá, eu estou feito doido tentando resolver umas questões mais eu não consigo, já vi videos no youtube e não consegui compreender muito...
Eu queria que responde-sem essas questões
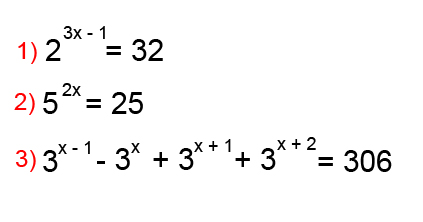
-
riickscrotzze
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Ter Jun 04, 2013 15:40
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Edificalçoes
- Andamento: cursando
 por Rafael16 » Ter Jun 04, 2013 17:57
por Rafael16 » Ter Jun 04, 2013 17:57
-
Rafael16
- Colaborador Voluntário

-
- Mensagens: 154
- Registrado em: Qui Mar 01, 2012 22:24
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Análise de Sistemas
- Andamento: cursando
 por riickscrotzze » Ter Jun 04, 2013 18:15
por riickscrotzze » Ter Jun 04, 2013 18:15

eu não entendi pq deu 34
Pode explicar, grato
-
riickscrotzze
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Ter Jun 04, 2013 15:40
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Edificalçoes
- Andamento: cursando
 por riickscrotzze » Ter Jun 04, 2013 18:17
por riickscrotzze » Ter Jun 04, 2013 18:17
Outra coisa que vc poderia responder, caso vc saiba...
viewtopic.php?f=108&t=12313link ai em cima
-
riickscrotzze
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Ter Jun 04, 2013 15:40
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Edificalçoes
- Andamento: cursando
 por Rafael16 » Ter Jun 04, 2013 22:23
por Rafael16 » Ter Jun 04, 2013 22:23
Somei, veja:
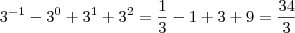
-
Rafael16
- Colaborador Voluntário

-
- Mensagens: 154
- Registrado em: Qui Mar 01, 2012 22:24
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Análise de Sistemas
- Andamento: cursando
 por riickscrotzze » Qua Jun 05, 2013 13:53
por riickscrotzze » Qua Jun 05, 2013 13:53
Ah, agora eu consegui compreender
Obrigado


-
riickscrotzze
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Ter Jun 04, 2013 15:40
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Edificalçoes
- Andamento: cursando
Voltar para Equações
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Alguem consegue resolver esse limite?
por priscila1992 » Dom Abr 15, 2012 17:26
- 1 Respostas
- 1455 Exibições
- Última mensagem por LuizAquino

Seg Abr 16, 2012 15:09
Cálculo: Limites, Derivadas e Integrais
-
- [Logaritmos] Alguém consegue resolver essas questões?
por riickscrotzze » Ter Jun 04, 2013 16:05
- 2 Respostas
- 2139 Exibições
- Última mensagem por riickscrotzze

Qua Jun 05, 2013 13:54
Logaritmos
-
- Alguém consegue?
por robsonwendel » Ter Set 13, 2016 01:39
- 1 Respostas
- 3614 Exibições
- Última mensagem por Cleyson007

Ter Set 13, 2016 15:48
Cálculo: Limites, Derivadas e Integrais
-
- Alguem me ajuda nessa equação exponencial
por raphael11234 » Qua Jun 08, 2016 00:07
- 1 Respostas
- 4724 Exibições
- Última mensagem por Cleyson007

Qua Jun 08, 2016 15:20
Equações
-
- Consegue resolver o limite?
por Cleyson007 » Sáb Abr 28, 2012 17:18
- 1 Respostas
- 1260 Exibições
- Última mensagem por MarceloFantini

Dom Abr 29, 2012 14:59
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
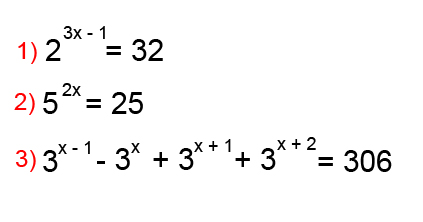

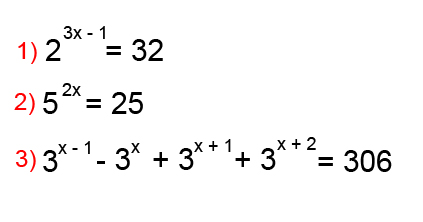

 o que implica em
o que implica em 



 ---> Coloquei o
---> Coloquei o 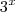 em evidência
em evidência








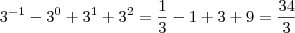




 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.