A apresentação de motociclistas, dentro do globo da
morte, é sempre um momento empolgante de uma
sessão de circo, pois, ao atingir o ponto mais alto do
globo, eles ficam de ponta cabeça. Para que, nesse
momento, o motociclista não caia, é necessário que ele
esteja a uma velocidade mínima (v) que se relaciona com
o raio do globo (R) e a aceleração da gravidade (g) pela
expressão: , com R dado em metros.
VESTIBULINHO 1
o
SEM/15
•
Etec
14
A apresentação de motociclistas, dentro do globo da
morte, é sempre um momento empolgante de uma
sessão de circo, pois, ao atingir o ponto mais alto do
globo, eles ficam de ponta cabeça. Para que, nesse
momento, o motociclista não caia, é necessário que ele
esteja a uma velocidade mínima (v) que se relaciona com
o raio do globo (R) e a aceleração da gravidade (g) pela
expressão: , com R dado em metros.
Considere que no ponto mais alto de um globo da morte,
um motociclista não caiu, pois estava com a velocidade
mínima de 27 km/h.
Assim sendo, o raio do globo é, aproximadamente, em
metros,
(A)
5,6.
(B)
6,3.
(C)
7,5.
(D)
8,2.
(E)
9,8
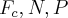,onde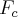 
força centripeta,N normal,P peso de forma q.
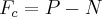...aqui N=0,pois a velocidade sera minima...logo...
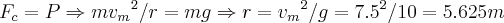...v=27/3.6=7.5m/s
