Determine
 de modo que a equação
de modo que a equação 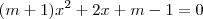 tenhas raízes positivas gabarito :
tenhas raízes positivas gabarito : 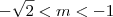

 de modo que a equação
de modo que a equação 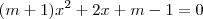 tenhas raízes positivas gabarito :
tenhas raízes positivas gabarito : 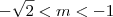

 + 2x + (m - 1), achando o valor de delta:
+ 2x + (m - 1), achando o valor de delta: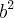 - 4 . a . c ---> 4 - 4 (m + 1) (m - 1) ---> - 4
- 4 . a . c ---> 4 - 4 (m + 1) (m - 1) ---> - 4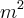 + 8, porém, para termos raízes teremos que ter delta maior que zero: - 4
+ 8, porém, para termos raízes teremos que ter delta maior que zero: - 4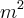 + 8 > 0 ---> m > ?
+ 8 > 0 ---> m > ? ![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) , como o valor positivo não é maior que zero então, usamos o valor negativo: m >-
, como o valor positivo não é maior que zero então, usamos o valor negativo: m >- ![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) .
.![x1 = \frac{- b + \sqrt[]{\Delta}}{2a} x1 = \frac{- b + \sqrt[]{\Delta}}{2a}](/latexrender/pictures/d8da6fbb638ed89d4638f04845175998.png) , e
, e ![x2 = \frac{- b - \sqrt[]{\Delta}}{2a} x2 = \frac{- b - \sqrt[]{\Delta}}{2a}](/latexrender/pictures/b6cc4720a8f93f43a8c064463d675975.png) , donde vem que: 2a = 2m + 2 > 0 ---> m > -1 ou 2a = 2m + 2 < 0 ---> m < -1, como o primeiro valor de m que encontramos era -
, donde vem que: 2a = 2m + 2 > 0 ---> m > -1 ou 2a = 2m + 2 < 0 ---> m < -1, como o primeiro valor de m que encontramos era -![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) então, o valor que encaixa com a resposta é m < -1. Pois, se o contrário ocorresse então, excluiríamos o primeiro valor de m > -
então, o valor que encaixa com a resposta é m < -1. Pois, se o contrário ocorresse então, excluiríamos o primeiro valor de m > -![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) .
.![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) < m < -1}.
< m < -1}.
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante

 .
.



