 por Thiago 86 » Ter Mar 12, 2013 15:00
por Thiago 86 » Ter Mar 12, 2013 15:00
Saldações

, estou respondendo uma questão e infelismente não consigo descobrí onde estou errando.
Para que valores de "m" a equação
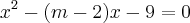
, admite raizes reais simétricas.
1° dúvida. O termo simetria usado, significa igualdade?
Como eu tentei:
![{x}^{2} - (m-2)x-9=0
\Delta=0
{[-(m-2)]}^{2} - 4.1.(-9)=0
{m}^{2} -4m+4+36=0
{m}^{2} -4m+40=0
\Delta={-4}^{2} -4.1.40
\Delta=16-160
\Delta=-144??? {x}^{2} - (m-2)x-9=0
\Delta=0
{[-(m-2)]}^{2} - 4.1.(-9)=0
{m}^{2} -4m+4+36=0
{m}^{2} -4m+40=0
\Delta={-4}^{2} -4.1.40
\Delta=16-160
\Delta=-144???](/latexrender/pictures/73ebd5180ac87d0a253a44a107e4465c.png)
-
Thiago 86
- Usuário Dedicado

-
- Mensagens: 40
- Registrado em: Seg Fev 11, 2013 18:55
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Curso técnico em enfermagem
- Andamento: cursando
 por Russman » Ter Mar 12, 2013 16:49
por Russman » Ter Mar 12, 2013 16:49
Não! Números simétricos tem o mesmo módulo, mas sinais opostos. O simétrico de

é
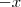
.
Assim, as raízes da equação tem de ser

e
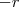
. Há diversas formas de resolver essa questão. Optei por esta:
A equação tem raízes

e
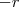
. Assim, podemos escreve-la como
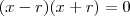
de forma que
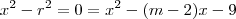
.
Por igualdade de polinômios, temos, então
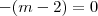
, de onde
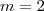
, e
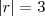
.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por Thiago 86 » Qua Mar 13, 2013 09:39
por Thiago 86 » Qua Mar 13, 2013 09:39
Saudações

.
Descupe-me, mas eu não sei o que é números simétricose.
Eu estou estudando matemática sozinho, desde o início com uma apostila, e estou vendo que ela tem algumas falhas se você tivesse algum material falando sobrre simetria que pudece me enviar ficaria agradecido.
Voltando para a questão, é por isso que eu não consegui entender porque x=-x.
Desde já muito obrigado.
-
Thiago 86
- Usuário Dedicado

-
- Mensagens: 40
- Registrado em: Seg Fev 11, 2013 18:55
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Curso técnico em enfermagem
- Andamento: cursando
Voltar para Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 , estou respondendo uma questão e infelismente não consigo descobrí onde estou errando.
, estou respondendo uma questão e infelismente não consigo descobrí onde estou errando.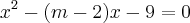 , admite raizes reais simétricas.
, admite raizes reais simétricas.![{x}^{2} - (m-2)x-9=0
\Delta=0
{[-(m-2)]}^{2} - 4.1.(-9)=0
{m}^{2} -4m+4+36=0
{m}^{2} -4m+40=0
\Delta={-4}^{2} -4.1.40
\Delta=16-160
\Delta=-144??? {x}^{2} - (m-2)x-9=0
\Delta=0
{[-(m-2)]}^{2} - 4.1.(-9)=0
{m}^{2} -4m+4+36=0
{m}^{2} -4m+40=0
\Delta={-4}^{2} -4.1.40
\Delta=16-160
\Delta=-144???](/latexrender/pictures/73ebd5180ac87d0a253a44a107e4465c.png)

 , estou respondendo uma questão e infelismente não consigo descobrí onde estou errando.
, estou respondendo uma questão e infelismente não consigo descobrí onde estou errando.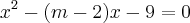 , admite raizes reais simétricas.
, admite raizes reais simétricas.![{x}^{2} - (m-2)x-9=0
\Delta=0
{[-(m-2)]}^{2} - 4.1.(-9)=0
{m}^{2} -4m+4+36=0
{m}^{2} -4m+40=0
\Delta={-4}^{2} -4.1.40
\Delta=16-160
\Delta=-144??? {x}^{2} - (m-2)x-9=0
\Delta=0
{[-(m-2)]}^{2} - 4.1.(-9)=0
{m}^{2} -4m+4+36=0
{m}^{2} -4m+40=0
\Delta={-4}^{2} -4.1.40
\Delta=16-160
\Delta=-144???](/latexrender/pictures/73ebd5180ac87d0a253a44a107e4465c.png)

 é
é 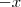 .
. e
e 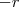 . Há diversas formas de resolver essa questão. Optei por esta:
. Há diversas formas de resolver essa questão. Optei por esta: e
e 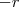 . Assim, podemos escreve-la como
. Assim, podemos escreve-la como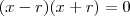
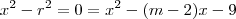 .
.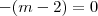 , de onde
, de onde 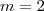 , e
, e 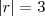 .
.
 .
.





