quando eu chamo , por exemplo ,
 , em uma equação exponencial , que depois cai em uma equação do 2°
, em uma equação exponencial , que depois cai em uma equação do 2° grau , dai eu acho o x' e o x'' , que por exemplo são 2 e 1 , dai eu tenho que substituir o 2 e 1 assim
 ou assim
ou assim  ( tenho que colocar o 2 e 1 no lugar do x ou do y ?
( tenho que colocar o 2 e 1 no lugar do x ou do y ?

 deve substituir os valores em
deve substituir os valores em  , em
, em 

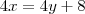
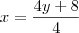

 .
.

 .
.



