Estou com outro problema de interpretação. O exercício diz o seguinte:
"Dispomos de 8 cores e queremos pintar uma bandeira de 5 listras, cada listra com uma cor. De quantas formas isto pode ser feito ?"
A princípio, pensei que tínhamos 8 opções para cada listra e, então a resposta seria 8.8.8.8.8, porém está errado. Daí, percebi que duas listras juntas não poderiam ter a mesma cor (é claro). Por outro lado, a resolução sugere que seja feito 8.7.6.5.4, mas, pelo menos para mim, não ficou claro que todas as listras tinham que ter cores distintas umas das outras. Se estivesse escrito "..., cada listra com uma cor distinta. ..." então, estaria esclarecido que as cores não podiam ser repetidas. Eu estou errada ? Devia ter interpretado como cores todas distintas ? Por favor, ajudem-me.



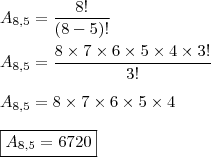



 , avisa que eu resolvo.
, avisa que eu resolvo.

