O prêmio de um concurso no valor de R$ 490.000,00 deverá ser divido de forma diretamente proporcional aos pontos obtidos pelos candidatos das três primeiras colocações. Considerando que o primeiro colocado fez 220, o segundo 150 e o terceiro 120 pontos, determine a parte do prêmio relativa a cada participante.
Respostas: R$ 176.000,00, R$ 120.000,00 e R$ 96.000,00, ( eu acho que essa resposta do gabarito está errada, pois eu não consigo chegar a ela .Ma se alguém conseguir por favor me ajude)


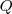 é o valor que o candidato deve receber em função do número
é o valor que o candidato deve receber em função do número  de pontos que fez e ambas quantidades são diretamente proporcionais deve existir uma constante
de pontos que fez e ambas quantidades são diretamente proporcionais deve existir uma constante  tal que
tal que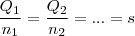
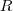 , será totalmente dividido entre os ganhadores, temos
, será totalmente dividido entre os ganhadores, temos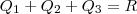
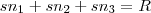
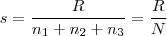 .
.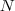 é a soma dos pontos dos 3 candidatos.
é a soma dos pontos dos 3 candidatos.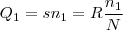
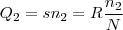
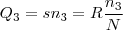
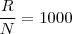 . kk
. kk

 , avisa que eu resolvo.
, avisa que eu resolvo.

