 por Pessoa Estranha » Seg Ago 26, 2013 18:09
por Pessoa Estranha » Seg Ago 26, 2013 18:09
Olá Pessoal, gostaria de ajuda para calcular a seguinte equação logarítmica:
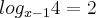
.
Fiz o seguinte:
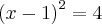
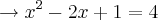
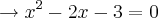
.
Aplicando Bháskara:
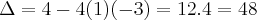
![\rightarrow {x}_{1}=\frac{2+\sqrt[2]{48}}{2}= \rightarrow {x}_{1}=\frac{2+\sqrt[2]{48}}{2}=](/latexrender/pictures/3bad29dee697b8b9f80f2c6ffc909663.png)
![\frac{2(1+2\sqrt[2]{3})}{2}=1+2\sqrt[2]{3} \frac{2(1+2\sqrt[2]{3})}{2}=1+2\sqrt[2]{3}](/latexrender/pictures/5cb9382d00271608fbb7f8cc579e2396.png)
e
![{x}_{2}=1-2\sqrt[2]{3} {x}_{2}=1-2\sqrt[2]{3}](/latexrender/pictures/1c3d1ca56935cf58d683031cb0c46fc7.png)
.
Porém testando estes valores, não há como afirmar que estes valores para x estão corretos.
Outra maneira de fazer, que dá certo, é:
![{(x-1)}^{2}=4\rightarrow x-1=\sqrt[2]{4} {(x-1)}^{2}=4\rightarrow x-1=\sqrt[2]{4}](/latexrender/pictures/d09662607d18874c9dea136b8f5a7bd6.png)
Daí:
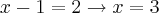
ou
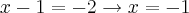
Logo, S={3}, pois x=-1 não satisfaz a condição de existência do logaritmo, tal que a base deve ser positiva e diferente de 1.
Eu gostaria de saber o motivo pelo qual a primeira resolução não funciona, ou qual é o erro nela.
Obrigada!
-
Pessoa Estranha
- Colaborador Voluntário

-
- Mensagens: 262
- Registrado em: Ter Jul 16, 2013 16:43
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por Russman » Seg Ago 26, 2013 18:57
por Russman » Seg Ago 26, 2013 18:57
Você calculou o

errado.

e não

.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por Pessoa Estranha » Seg Ago 26, 2013 22:01
por Pessoa Estranha » Seg Ago 26, 2013 22:01
Obrigada....

(quanta falta de atenção....)
-
Pessoa Estranha
- Colaborador Voluntário

-
- Mensagens: 262
- Registrado em: Ter Jul 16, 2013 16:43
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
Voltar para Aritmética
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Equação logaritmica
por DanielRJ » Qui Out 07, 2010 17:20
- 4 Respostas
- 2474 Exibições
- Última mensagem por DanielRJ

Sáb Out 09, 2010 15:28
Logaritmos
-
- (AFA) equação logaritmica
por natanskt » Sex Out 08, 2010 12:27
- 2 Respostas
- 1880 Exibições
- Última mensagem por Molina

Sex Out 08, 2010 14:30
Funções
-
- (AFA) equação logaritmica
por natanskt » Sex Out 08, 2010 12:30
- 1 Respostas
- 1463 Exibições
- Última mensagem por DanielRJ

Sex Out 08, 2010 14:13
Funções
-
- (AFA) Equação logaritmica
por natanskt » Sáb Out 09, 2010 13:31
- 1 Respostas
- 1678 Exibições
- Última mensagem por DanielRJ

Sáb Out 09, 2010 13:42
Logaritmos
-
- (AFA) Equação logaritmica
por natanskt » Sáb Out 09, 2010 14:51
- 2 Respostas
- 1828 Exibições
- Última mensagem por natanskt

Seg Out 11, 2010 15:58
Logaritmos
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
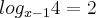 .
.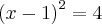
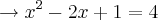
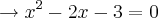 .
.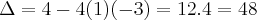
![\rightarrow {x}_{1}=\frac{2+\sqrt[2]{48}}{2}= \rightarrow {x}_{1}=\frac{2+\sqrt[2]{48}}{2}=](/latexrender/pictures/3bad29dee697b8b9f80f2c6ffc909663.png)
![\frac{2(1+2\sqrt[2]{3})}{2}=1+2\sqrt[2]{3} \frac{2(1+2\sqrt[2]{3})}{2}=1+2\sqrt[2]{3}](/latexrender/pictures/5cb9382d00271608fbb7f8cc579e2396.png) e
e ![{x}_{2}=1-2\sqrt[2]{3} {x}_{2}=1-2\sqrt[2]{3}](/latexrender/pictures/1c3d1ca56935cf58d683031cb0c46fc7.png) .
.![{(x-1)}^{2}=4\rightarrow x-1=\sqrt[2]{4} {(x-1)}^{2}=4\rightarrow x-1=\sqrt[2]{4}](/latexrender/pictures/d09662607d18874c9dea136b8f5a7bd6.png)
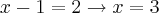
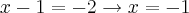


 errado.
errado.
 .
.