5) Um móvel percorre 30 km na primeira hora, 26 km na segunda hora e assim por diante em progressão aritmética. Para percorrer 120 km gastará
a) 5h
b) 6h
c) 7h
d) 8h
e) 10h
Gabarito
Eu não estou conseguindo resolver esse problema.
(30, 26, 22, ...)
a1= 30;
a2 = 26;
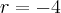
r = -4;
an = 120;
n = ?
an = a1 + (n-1).r
a120 = 30 + (120-1).(-4)
a120 = 30 + 119.(-4)
a120 = 30 - 476
a120 = -446
Eu tento continuar assim e nunca dá certo, estou ficando louco já com isso. Não quero desistir. Quero aprender como resolver pra poder entender melhor o processo.
Eu repensei aqui, e vi que a120 está incorreto porque não quer achar o a120 e sim achar qual a sequência das somas dos termos que dará 120km. Mais não consigo desenvolver o exercício.



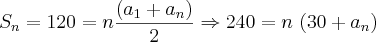

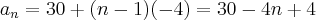
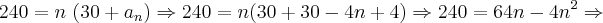



![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.