 por douglasmacbrito » Ter Mar 26, 2013 14:07
por douglasmacbrito » Ter Mar 26, 2013 14:07
5) Um móvel percorre 30 km na primeira hora, 26 km na segunda hora e assim por diante em progressão aritmética. Para percorrer 120 km gastará
a) 5h
b) 6h
c) 7h
d) 8h
e) 10h
Gabarito
Eu não estou conseguindo resolver esse problema.
(30, 26, 22, ...)
a1= 30;
a2 = 26;
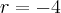
r = -4;
an = 120;
n = ?
an = a1 + (n-1).r
a120 = 30 + (120-1).(-4)
a120 = 30 + 119.(-4)
a120 = 30 - 476
a120 = -446
Eu tento continuar assim e nunca dá certo, estou ficando louco já com isso. Não quero desistir. Quero aprender como resolver pra poder entender melhor o processo.
Eu repensei aqui, e vi que a120 está incorreto porque não quer achar o a120 e sim achar qual a sequência das somas dos termos que dará 120km. Mais não consigo desenvolver o exercício.
-
douglasmacbrito
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Ter Mar 19, 2013 13:40
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por nakagumahissao » Ter Mar 26, 2013 14:58
por nakagumahissao » Ter Mar 26, 2013 14:58
Veja bem, o móvel percorreu 30 km na primeira hora, 26 km na segunda hora e assim por diante em PA. Veja que a pergunta feita, solicita que você encontre o tempo total para percorrer 120 km. Repare que todos os dados são em km (30, 26,...) e em um determinado momento a SOMA total dos quilômetros percorridos deverá atingir 120 km.
O erro foi em considerar n = 120 km, pois neste caso, n é o tempo. Assim:

Equação I:
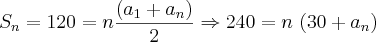
Temos uma equação com duas variáveis aqui. Precisaremos eliminar um deles. Lembramos que:

e
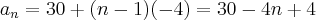
Substituindo o resultado acima na Equação I, teremos
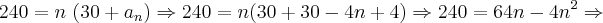
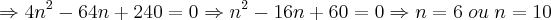
Agora raciocinemos um pouco. Se:

e

Assim, não iremos considerar quilometragens negativas e aceitar que o tempo necessário será de 6 Horas. Portanto a resposta será (b) = 6 h
Eu faço a diferença. E você?
Do Poema: Quanto os professores "fazem"?
De Taylor Mali
-
nakagumahissao
- Colaborador Voluntário

-
- Mensagens: 386
- Registrado em: Qua Abr 04, 2012 14:07
- Localização: Brazil
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Lic. Matemática
- Andamento: cursando
-
 por douglasmacbrito » Ter Mar 26, 2013 18:33
por douglasmacbrito » Ter Mar 26, 2013 18:33
Muito obrigado amigo por ter me ajudado.
-
douglasmacbrito
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Ter Mar 19, 2013 13:40
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
Voltar para Aritmética
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- P.A nao consigo resolver essa p.a.
por Dalila » Sex Nov 14, 2008 16:58
- 2 Respostas
- 3140 Exibições
- Última mensagem por admin

Sex Nov 14, 2008 17:29
Progressões
-
- [Conjuntos] Não consigo resolver.
por Ambrosio » Qui Ago 25, 2011 22:36
- 1 Respostas
- 1978 Exibições
- Última mensagem por Neperiano

Sex Ago 26, 2011 12:28
Álgebra Elementar
-
- Não consigo resolver, me ajude!
por Pinho » Qua Nov 02, 2011 11:00
- 0 Respostas
- 1114 Exibições
- Última mensagem por Pinho

Qua Nov 02, 2011 11:00
Polinômios
-
- [calculo] não consigo resolver
por jaques » Seg Nov 28, 2011 01:02
- 1 Respostas
- 1360 Exibições
- Última mensagem por TheoFerraz

Seg Nov 28, 2011 15:14
Álgebra Elementar
-
- 3 questões de Binômio que não consigo resolver! =/
por Giles » Qua Nov 05, 2008 19:31
- 2 Respostas
- 6057 Exibições
- Última mensagem por Molina

Qui Nov 06, 2008 00:40
Binômio de Newton
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.




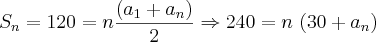

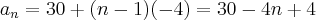
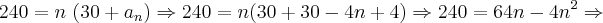
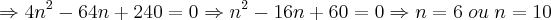





 substitui-se
substitui-se 
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.