 por Lucio » Sex Nov 02, 2012 19:47
por Lucio » Sex Nov 02, 2012 19:47
Olá Colegas...
A média aritmética entre
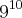
,
![\sqrt[]{{3}^{40}} \sqrt[]{{3}^{40}}](/latexrender/pictures/23be68ade85a47b1203dcb8204d7c07b.png)
e
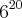
é igual a?
A resposta é
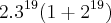
Tentei resolver assim:
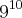
+
![\sqrt[]{{3}^{40}} \sqrt[]{{3}^{40}}](/latexrender/pictures/23be68ade85a47b1203dcb8204d7c07b.png)
+
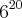
=
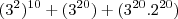
=
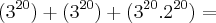
Minha dúvida é a partir de agora, coloquei
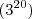
porém não consigo chegar na resposta.
Desde já agradeço a atenção de todos
Um abraço
-
Lucio
- Usuário Dedicado

-
- Mensagens: 29
- Registrado em: Qua Dez 21, 2011 07:15
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática
- Andamento: cursando
 por e8group » Sex Nov 02, 2012 20:09
por e8group » Sex Nov 02, 2012 20:09
Fiz assim ,
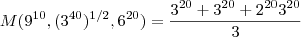
. Colocando o fator 3 em evidência no numerador e cancelando com o mesmo no denominador , fica :

Daí ,
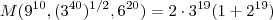
.
Note q vc só esqueceu de dividir por três .
Em geral :
[tex\]bar{x} = \frac{ x_1 + x_2 + \hdots + x_n }{n}[/tex] .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Lucio » Sex Nov 02, 2012 23:55
por Lucio » Sex Nov 02, 2012 23:55
Santhiago, muito obrigado pelo seu auxílio.
-
Lucio
- Usuário Dedicado

-
- Mensagens: 29
- Registrado em: Qua Dez 21, 2011 07:15
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática
- Andamento: cursando
Voltar para Aritmética
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Prova por Indução] Progressão Aritmético-Geométrica
por MateusDantas1 » Qui Fev 16, 2012 15:07
- 10 Respostas
- 7492 Exibições
- Última mensagem por Victor Neumann

Qui Fev 23, 2012 21:57
Progressões
-
- P.A - Média
por DanielFerreira » Qua Jul 29, 2009 15:30
- 2 Respostas
- 2670 Exibições
- Última mensagem por DanielFerreira

Qui Jul 30, 2009 17:27
Progressões
-
- média
por Andreza » Qui Nov 24, 2011 13:03
- 3 Respostas
- 2617 Exibições
- Última mensagem por Neperiano

Sex Nov 25, 2011 10:15
Estatística
-
- média
por Italo de Souza » Sáb Out 11, 2014 11:09
- 4 Respostas
- 6859 Exibições
- Última mensagem por jcmatematica

Dom Out 12, 2014 02:27
Teoria dos Números
-
- Média Aritmética
por gustavowelp » Seg Jun 28, 2010 11:17
- 1 Respostas
- 2376 Exibições
- Última mensagem por Douglasm

Seg Jun 28, 2010 12:09
Estatística
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
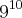 ,
,![\sqrt[]{{3}^{40}} \sqrt[]{{3}^{40}}](/latexrender/pictures/23be68ade85a47b1203dcb8204d7c07b.png) e
e 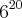 é igual a?
é igual a?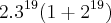
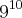 +
+ ![\sqrt[]{{3}^{40}} \sqrt[]{{3}^{40}}](/latexrender/pictures/23be68ade85a47b1203dcb8204d7c07b.png) +
+ 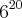 =
= 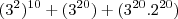 =
=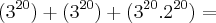
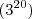 porém não consigo chegar na resposta.
porém não consigo chegar na resposta.
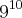 ,
,![\sqrt[]{{3}^{40}} \sqrt[]{{3}^{40}}](/latexrender/pictures/23be68ade85a47b1203dcb8204d7c07b.png) e
e 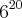 é igual a?
é igual a?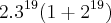
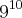 +
+ ![\sqrt[]{{3}^{40}} \sqrt[]{{3}^{40}}](/latexrender/pictures/23be68ade85a47b1203dcb8204d7c07b.png) +
+ 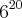 =
= 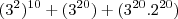 =
=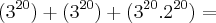
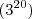 porém não consigo chegar na resposta.
porém não consigo chegar na resposta.
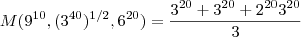 . Colocando o fator 3 em evidência no numerador e cancelando com o mesmo no denominador , fica :
. Colocando o fator 3 em evidência no numerador e cancelando com o mesmo no denominador , fica : 
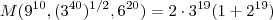 .
. 



 , avisa que eu resolvo.
, avisa que eu resolvo.

