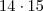-
-
Novo APOIA.se AjudaMatemática
por admin em Sáb Abr 25, 2020 19:01
- 0 Tópicos
- 480523 Mensagens
-
Última mensagem por admin

em Sáb Abr 25, 2020 19:01
-
-
Agradecimento aos Colaboradores
por admin em Qui Nov 15, 2018 00:25
- 0 Tópicos
- 541196 Mensagens
-
Última mensagem por admin

em Qui Nov 15, 2018 00:25
-
-
Ativação de Novos Registros
por admin em Qua Nov 14, 2018 11:58
- 0 Tópicos
- 504997 Mensagens
-
Última mensagem por admin

em Qua Nov 14, 2018 11:58
-
-
Regras do Fórum - Leia antes de postar!
por admin em Ter Mar 20, 2012 21:51
- 0 Tópicos
- 731972 Mensagens
-
Última mensagem por admin

em Ter Mar 20, 2012 21:51
-
-
DICA: Escrevendo Fórmulas com LaTeX via BBCode
por admin em Qua Ago 29, 2007 04:04
- 41 Tópicos
- 2173289 Mensagens
-
Última mensagem por Janayna

em Qui Abr 27, 2017 00:04
 por willmorais » Ter Fev 09, 2016 14:36
por willmorais » Ter Fev 09, 2016 14:36
Boa tarde,
Eu sou da área de humanas, então tenho muita dificuldade em questões de matemática. Se puderem me ajudar a responder a questão abaixo, agradeço. Pelo menos explicar como vou excluindo as alternativas, pois eu não sei por onde começar. Obrigado!
(UFES 2013) 12ª QUESTÃO - Sejam x e y números reais positivos. Pode-se garantir que:A) Não existem x e y irracionais tais que x^2 ? y é racional.
B) Existem x inteiro e y racional tal que x ? y é irracional.
C) Para todo x racional e para todo y irracional, tem-se que x ? y^2 é racional.
D) Se x e y são inteiros e x ? y é divisível por um número inteiro z, então x é divisível por z ou y é divisível
por z.
E) Para todo x racional e para todo y irracional, tem-se que x^2 +
![\sqrt[]{y} \sqrt[]{y}](/latexrender/pictures/2c7054a0a5416b35c805d1e6e3dc1a54.png)
é irracional.
-
willmorais
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Ter Fev 09, 2016 14:18
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Jornalismo
- Andamento: formado
 por e8group » Qua Fev 10, 2016 11:27
por e8group » Qua Fev 10, 2016 11:27
(a) Falsa . Basta escolher qualquer número irracional

(e.g.
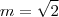
) .Ora ,
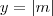
e
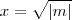
são irracionais tais que
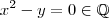
(b) Falsa . Basta notar que

é fechado com respeito a soma e multiplicação ( i.e.
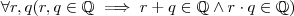
e que todo número inteiro é racional .
(c) Falsa : Tome por exemplo
![x = 0 , y = \sqrt[4]{2} x = 0 , y = \sqrt[4]{2}](/latexrender/pictures/c891f312d1dbe1deb2365b8ef65ac5f6.png)
(d) Falsa : Seria verdadeira sse tais inteiros fossem coprimos . Exemplo 6 não divide 14 e 15 mas divide
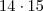
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Teoria dos Números
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Teoria Números] Algoritmo Não Interceptação Números Primos
por WillamesSilva » Qua Out 26, 2016 12:21
- 8 Respostas
- 15103 Exibições
- Última mensagem por WillamesSilva

Ter Nov 22, 2016 15:33
Aritmética
-
- Teoria dos Números
por cheese » Sáb Out 24, 2009 14:08
- 1 Respostas
- 1916 Exibições
- Última mensagem por Cleyson007

Sáb Out 24, 2009 15:10
Álgebra Elementar
-
- Teoria dos números!
por Abelardo » Qui Mar 10, 2011 01:44
- 0 Respostas
- 1308 Exibições
- Última mensagem por Abelardo

Qui Mar 10, 2011 01:44
Álgebra Elementar
-
- Teoria dos Números
por felipemaster » Qua Jul 06, 2011 12:26
- 1 Respostas
- 1748 Exibições
- Última mensagem por MarceloFantini

Qua Jul 06, 2011 19:41
Álgebra Elementar
-
- Teoria dos Números
por Jamyson » Seg Jan 21, 2013 19:28
- 1 Respostas
- 3303 Exibições
- Última mensagem por young_jedi

Qui Jan 24, 2013 21:49
Teoria dos Números
Usuários navegando neste fórum: Nenhum usuário registrado e 7 visitantes
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\sqrt[]{y} \sqrt[]{y}](/latexrender/pictures/2c7054a0a5416b35c805d1e6e3dc1a54.png) é irracional.
é irracional.

 (e.g.
(e.g. 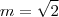 ) .Ora ,
) .Ora , 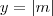 e
e 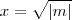 são irracionais tais que
são irracionais tais que 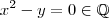
 é fechado com respeito a soma e multiplicação ( i.e.
é fechado com respeito a soma e multiplicação ( i.e. 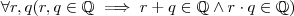 e que todo número inteiro é racional .
e que todo número inteiro é racional .![x = 0 , y = \sqrt[4]{2} x = 0 , y = \sqrt[4]{2}](/latexrender/pictures/c891f312d1dbe1deb2365b8ef65ac5f6.png)