Sejam os pares Ai ?
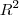 , i = 1, 2, 3, 4, 5 que sao as coordenadas planares de cinco antenas de celulares. Seja (a, b) ?
, i = 1, 2, 3, 4, 5 que sao as coordenadas planares de cinco antenas de celulares. Seja (a, b) ? 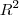 as coordenadas planares de um telefone celular. Seja a relacao R ?
as coordenadas planares de um telefone celular. Seja a relacao R ? 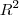 ×
× 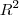 . Dois telefones de coordenadas planares c1 ?
. Dois telefones de coordenadas planares c1 ? 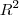 et c2 ?
et c2 ? 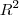 estarao em relacao se a antena mais proxima de cada um é a mesma. Teremos entao c1 R c2. Mostrar que esta relacao é uma relacao de equivalencia.
estarao em relacao se a antena mais proxima de cada um é a mesma. Teremos entao c1 R c2. Mostrar que esta relacao é uma relacao de equivalencia.


 .
.
 :
: