-
-
Novo APOIA.se AjudaMatemática
por admin em Sáb Abr 25, 2020 19:01
- 0 Tópicos
- 478879 Mensagens
-
Última mensagem por admin

em Sáb Abr 25, 2020 19:01
-
-
Agradecimento aos Colaboradores
por admin em Qui Nov 15, 2018 00:25
- 0 Tópicos
- 536512 Mensagens
-
Última mensagem por admin

em Qui Nov 15, 2018 00:25
-
-
Ativação de Novos Registros
por admin em Qua Nov 14, 2018 11:58
- 0 Tópicos
- 500238 Mensagens
-
Última mensagem por admin

em Qua Nov 14, 2018 11:58
-
-
Regras do Fórum - Leia antes de postar!
por admin em Ter Mar 20, 2012 21:51
- 0 Tópicos
- 719380 Mensagens
-
Última mensagem por admin

em Ter Mar 20, 2012 21:51
-
-
DICA: Escrevendo Fórmulas com LaTeX via BBCode
por admin em Qua Ago 29, 2007 04:04
- 41 Tópicos
- 2145625 Mensagens
-
Última mensagem por Janayna

em Qui Abr 27, 2017 00:04
 por Hanna bella14 » Dom Mai 22, 2016 17:48
por Hanna bella14 » Dom Mai 22, 2016 17:48
Para produzir morangos,um agricultor utilizada um terreno retangular com as dimensões 20 m por 30 m. Com o objetivo de aumentar a área do plantio, o agricultor decidiu aumentar o terreno em x metros na largura e x+8 no comprimento . Qual deve ser o valor de x para que a área do plantio seja aumentada em 1000metros quadrados?
-
Hanna bella14
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Qua Mai 18, 2016 14:39
- Formação Escolar: ENSINO FUNDAMENTAL II
- Andamento: cursando
 por adauto martins » Qua Mai 25, 2016 16:56
por adauto martins » Qua Mai 25, 2016 16:56
a area anterior era de
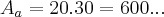
a area a ser acrescentada sera de 400,logo é resolver a equaçao...

...
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
Voltar para Lógica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Razão da área do triângulo para a área do quadrilátero]
 por Mayra Luna » Sex Nov 23, 2012 20:17
por Mayra Luna » Sex Nov 23, 2012 20:17
- 2 Respostas
- 3992 Exibições
- Última mensagem por Mayra Luna

Ter Nov 27, 2012 14:53
Geometria Plana
-
- Área - Na próxima figura ABCD é um quadrilátero de área 200
 por marguiene » Sex Out 10, 2014 10:22
por marguiene » Sex Out 10, 2014 10:22
- 0 Respostas
- 1862 Exibições
- Última mensagem por marguiene

Sex Out 10, 2014 10:22
Geometria Plana
-
- Área - Na figura abaixo ABCD é um retângulo de área 11 cm².
 por marguiene » Sex Out 10, 2014 10:35
por marguiene » Sex Out 10, 2014 10:35
- 0 Respostas
- 2614 Exibições
- Última mensagem por marguiene

Sex Out 10, 2014 10:35
Geometria Plana
-
- [Área] Área de triangulo e trapézio
 por smlspirit » Qui Jul 19, 2012 20:07
por smlspirit » Qui Jul 19, 2012 20:07
- 1 Respostas
- 2684 Exibições
- Última mensagem por e8group

Qui Jul 19, 2012 20:57
Geometria Plana
-
- Area
por karenblond » Qui Mar 25, 2010 17:19
- 6 Respostas
- 3699 Exibições
- Última mensagem por Molina

Ter Mar 30, 2010 00:35
Geometria Plana
Usuários navegando neste fórum: Nenhum usuário registrado e 12 visitantes
Assunto:
[calculo] derivada
Autor:
beel - Seg Out 24, 2011 16:59
Para derivar a função
(16-2x)(21-x).x
como é melhor fazer?
derivar primeiro sei la, ((16-2x)(21-x))' achar o resultado (y)
e depois achar (y.x)' ?
Assunto:
[calculo] derivada
Autor:
MarceloFantini - Seg Out 24, 2011 17:15
Você poderia fazer a distributiva e derivar como um polinômio comum.
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:26
Funciona da mesma forma que derivada de x.y.z, ou seja, x'.y.z+x.y'.z+x.y.z' substitui cada expressão pelas variáveis e x',y' e z' é derivada de cada um
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:31
derivada de (16-2x)=-2
derivada de (21-x)=-1
derivada de x=1
derivada de (16-2x)(21-x)x=-2.(21-x)x+(-1).(16-2x)x +1.(16-2x)(21-x)
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



 ...
...