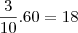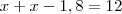por Tay » Seg Mar 18, 2013 13:46
por Tay » Seg Mar 18, 2013 13:46
Olá, não consigo resolver esse problema:
Ação global contra petróleo caro
A Agência Internacional de Energia (AIE), formada por
28 países, anunciou ontem a liberação de 60 milhões
de barris de petróleo de reservas estratégicas [...].
Os EUA vão entrar com metade do volume, [...] a
Europa irá colaborar com , e o restante virá de
Austrália, Japão, Coreia e Nova Zelândia.
O Globo, Rio de Janeiro, p. 17. 24 jun. 2011. Adaptado.
Suponha que os países asiáticos (Japão e Coreia) contribuam
juntos com 1,8 milhão de barris a mais do que
a contribuição total dos países da Oceania (Austrália e
Nova Zelândia).
Desse modo, quantos milhões de barris serão disponibilizados
pelos países asiáticos?
(A) 5,2
(B) 5,6
(C) 6,9
(D) 7,4
(E) 8,2
A resposta é C.
Pensei assim: 60 milhões, metade fica sob responsabilidade dos EUA (30 milhoes);
30 * 3/10 = 9 milhões da Europa
sobra 21 milhões para dividir para 4 países = 5,25 para cada país.
10,25 é a soma dos dois países mencionados, acrescido 1,8 milhões de barris que tais países irão pagar a mais que os outros dois: 8,7 - errado.
Alguém me ajuda, por favor?
A palavra é o meu domínio sobre o mundo.
-

Tay
- Usuário Ativo

-
- Mensagens: 23
- Registrado em: Seg Mar 18, 2013 13:24
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Letras
- Andamento: formado
 por young_jedi » Seg Mar 18, 2013 20:27
por young_jedi » Seg Mar 18, 2013 20:27
os estados unidos entrarão com 30 milhoes
ja a europa entrara com 3/10 do total ou seja
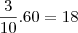
sobra então pra asia e oceania 30-18=12
temos então que a asia entrara com x, ja a oceania entrara com x-1,8
então
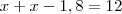
calcule e encontre x
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por Tay » Sex Mar 22, 2013 21:04
por Tay » Sex Mar 22, 2013 21:04

Deu 6,9 certinho.
Poxa, não ia conseguir fazer meesmo :(
Obrigada!

A palavra é o meu domínio sobre o mundo.
-

Tay
- Usuário Ativo

-
- Mensagens: 23
- Registrado em: Seg Mar 18, 2013 13:24
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Letras
- Andamento: formado
Voltar para Lógica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Questão cesgranrio
por Tay » Sáb Mar 30, 2013 17:33
- 19 Respostas
- 13355 Exibições
- Última mensagem por Tay

Sex Abr 12, 2013 22:22
Matemática Financeira
-
- Questão Cesgranrio
por Tay » Qua Abr 10, 2013 22:02
- 7 Respostas
- 6583 Exibições
- Última mensagem por Cleyson007

Ter Abr 16, 2013 07:47
Números Complexos
-
- Preciso de ajuda com essa questão da Fundação Cesgranrio
por Jesicaa » Qui Mar 12, 2015 11:46
- 2 Respostas
- 3156 Exibições
- Última mensagem por Jesicaa

Dom Mar 15, 2015 00:06
Sistemas de Equações
-
- Dúvida - Cesgranrio - Basa 2013
por Tay » Qui Jan 30, 2014 14:02
- 0 Respostas
- 1344 Exibições
- Última mensagem por Tay

Qui Jan 30, 2014 14:02
Matemática Financeira
-
- cesgranrio
por Maria Livia » Sex Set 06, 2013 10:15
- 0 Respostas
- 1518 Exibições
- Última mensagem por Maria Livia

Sex Set 06, 2013 10:15
Trigonometria
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.