 por zenildo » Ter Jul 14, 2015 19:47
por zenildo » Ter Jul 14, 2015 19:47
Um ônibus de 8 m de comprimento, deslocando-se com uma velocidade de 36 km/h atravessa uma ponte de 12 m de comprimento. Qual o tempo gasto pelo ônibus, em segundos, para atravessar totalmente a ponte?
a) 1
b) 2
c) 3
d) 4
Vm= ?r/?t ?3.6m/s= (r-r°)/?t?3.6m/s=(12-8)/?t??t=4/3.6, portanto: ?t=1s letra a.
-
zenildo
- Colaborador Voluntário

-
- Mensagens: 309
- Registrado em: Sáb Abr 06, 2013 20:12
- Localização: SALVADOR-BA, TERRA DO AXÉ! BAÊA!!!!!
- Formação Escolar: EJA
- Área/Curso: PRETENDO/ DIREITO
- Andamento: cursando
 por nakagumahissao » Qua Jul 15, 2015 10:23
por nakagumahissao » Qua Jul 15, 2015 10:23
Zenildo,
Posso estar errado, mas ao meu ver, o enunciado diz "para atravessar totalmente a ponte". Assim, quando o ônibus chegar ao fim da ponte, somente a frente terá atingido os 12 metros, ficando ainda 8 metros de ônibus ainda para passar, ou seja, para que
todo o ônibus tenha passado, ele deverá ter percorrido os 12 metros de ponte + os seus 8 metros, ficando 20 metros de percurso e assim:
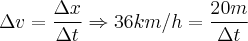
Vamos então transformar 36 km/h em metros por segundo. Assim:
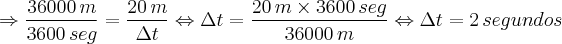

Eu faço a diferença. E você?
Do Poema: Quanto os professores "fazem"?
De Taylor Mali
-
nakagumahissao
- Colaborador Voluntário

-
- Mensagens: 386
- Registrado em: Qua Abr 04, 2012 14:07
- Localização: Brazil
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Lic. Matemática
- Andamento: cursando
-
Voltar para Lógica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Um ônibus...
por magaleao » Dom Dez 20, 2009 12:10
- 1 Respostas
- 2046 Exibições
- Última mensagem por Elcioschin

Seg Dez 21, 2009 18:17
Desafios Médios
-
- onibus
por junior_gyn » Seg Mai 09, 2011 00:45
- 1 Respostas
- 1932 Exibições
- Última mensagem por carlosalesouza

Seg Mai 09, 2011 09:14
Desafios Médios
-
- problema de pessoas no onibus
por hevhoram » Seg Mai 14, 2012 12:37
- 3 Respostas
- 2829 Exibições
- Última mensagem por DanielFerreira

Ter Mai 22, 2012 22:44
Álgebra Elementar
-
- [Lógica] Ônibus Lotado
por CJunior » Seg Out 06, 2014 15:52
- 3 Respostas
- 2118 Exibições
- Última mensagem por paulo testoni

Sáb Nov 01, 2014 16:35
Lógica
-
- Análise combinatória - Lugares ônibus
por rafapla » Seg Out 19, 2015 23:23
- 1 Respostas
- 7360 Exibições
- Última mensagem por DanielFerreira

Sáb Out 31, 2015 20:21
Análise Combinatória
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.




 .
.



