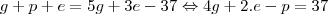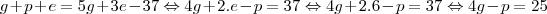por felipealves28 » Seg Jun 29, 2015 12:09
por felipealves28 » Seg Jun 29, 2015 12:09
Bom dia, gostaria de saber se consigo entrar com recurso nesta questão pois marquei C e no gabarito esta como A.
08 - Em um torneio de futebol amador, a cada rodada duas equipes se enfrentam. A equipe vitoriosa recebe 5 pontos e a perdedora não pontua; em caso de empate, cada uma das equipes recebe 3 pontos. Todos os pontos obtidos por uma equipe são somados, e aquele que tiver a maior pontuação no final do campeonato é declarado campeão. Sabendo que ao final do torneio a equipe dos Matemáticos obteve exatamente 37 pontos, considere as seguintes afirmativas: 1. A equipe dos Matemáticos jogou pelo menos 9 partidas nesse torneio. 2. A equipe dos Matemáticos obteve no máximo 6 empates. 3. A equipe dos Matemáticos foi derrotada pelo menos uma vez nesse torneio. Assinale a alternativa correta.
a) Somente a afirmativa 1 é verdadeira.
b) Somente as afirmativas 1 e 2 são verdadeiras.
c) Somente as afirmativas 1 e 3 são verdadeiras.
d) Somente as afirmativas 2 e 3 são verdadeiras.
e) As afirmativas 1, 2 e 3 são verdadeiras
Obrigado
-
felipealves28
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Seg Jun 29, 2015 11:59
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por nakagumahissao » Qua Ago 19, 2015 14:46
por nakagumahissao » Qua Ago 19, 2015 14:46
Supondo-se que T seja o total de pontos, g seja o número de rodadas ganhas, p, o número de rodadas perdidas e 'e' o número de rodadas empatadas temos:
5g + 0p + 3e = T
Como não foi dito quantas rodadas ocorreram e somente que T = 37, teremos:
5g + 0p + 3e = 37
Desde que g, p e e satisfaçam esta equação são válidas.
Opção 1: A equipe dos Matemáticos jogou pelo menos 9 partidas nesse torneio - Falso porque, comparando o número total de jogos com os de pontos,
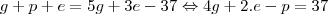
Se fosse p = 37 jogos, não haveriam pontos. Se fosse e = 37/2 = 18,5 e se fosse g = 37/4 = 9,02. Portanto, o número mínimo de jogos seria 10 para se ober 37 pontos.
Opção 2: A equipe dos Matemáticos obteve no máximo 6 empates. - Falso porque:
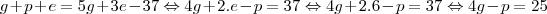
ou seja, depende de jogos que ganhou e que perdeu que podem ser qualquer valor, já que não foram informados.
Opção 3: A equipe dos Matemáticos foi derrotada pelo menos uma vez nesse torneio - Falso - Poderia ser 0.
Resposta: Na realidade, nenhuma seria verdadeira, mas como podemos arrendondar 9,02 para 9, considerarei qeu somente a 1 seja verdadeira.
Eu faço a diferença. E você?
Do Poema: Quanto os professores "fazem"?
De Taylor Mali
-
nakagumahissao
- Colaborador Voluntário

-
- Mensagens: 386
- Registrado em: Qua Abr 04, 2012 14:07
- Localização: Brazil
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Lic. Matemática
- Andamento: cursando
-
Voltar para Lógica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- concurso
 por nenocalmeida » Ter Mai 05, 2009 13:30
por nenocalmeida » Ter Mai 05, 2009 13:30
- 4 Respostas
- 3461 Exibições
- Última mensagem por rafagondi

Ter Mai 05, 2009 21:21
Conjuntos
-
- Concurso
por plugpc » Seg Ago 01, 2011 19:33
- 1 Respostas
- 2505 Exibições
- Última mensagem por LuizAquino

Ter Ago 02, 2011 17:51
Álgebra
-
- Problemas de concurso
por anapaulausp » Sex Jan 29, 2010 15:48
- 4 Respostas
- 4225 Exibições
- Última mensagem por anapaulausp

Seg Fev 01, 2010 10:00
Desafios Médios
-
- probleminha de concurso
por Alex farias » Ter Fev 02, 2010 21:00
- 4 Respostas
- 5448 Exibições
- Última mensagem por DanielFerreira

Seg Mar 15, 2010 13:09
Desafios Fáceis
-
- Questão de concurso...
por henrivoador » Seg Abr 19, 2010 20:37
- 7 Respostas
- 11309 Exibições
- Última mensagem por henrivoador

Seg Abr 26, 2010 13:07
Logaritmos
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.