 por Augusto Evaristo » Qua Nov 20, 2013 01:15
por Augusto Evaristo » Qua Nov 20, 2013 01:15
Muito bem. Você pensou na questão, e assim se aprende matemática. Pensando! Mas vamos pensar um pouco mais.
O n-esimo elemento (an) não pode ser 1550, pois este valor corresponde a quantidade de soldados. O primeiro elemento (a1) seria igual a 14, o número de soldados da primeira fila. Suas incógnitas são o numero de filas, n, e o n-esimo elemento, an.
an=a1+(n-1).r => an=14+(n-1).4
=> an=10-4.n
Sn=n. (a1+an)/2 => 1550=n. (14+an)/2
Substituindo an da 1a equação na 2a equação, temos:
1550=n. (14+10+4.n)/2, que dá em uma equação do segundo grau, n^2+6.n-775=0, cuja solução positiva é 25.
Logo, o total de filas a serem formadas são 25. Caso fosse pedido o e-nesimo elemento, era só substituir o valor de n em qualquer das duas primeiras equações.
Bons estudos!
Matemática não é uma arte
É a linguagem universal
Arte é conhece-la!


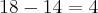
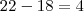

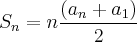
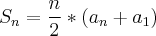
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)