 por mayconf » Seg Set 24, 2012 12:25
por mayconf » Seg Set 24, 2012 12:25
to com uma listinha aqui de Álgebra falta 2 exercício pra mim acaba mais ta difícil esses kkk se alguém puder me ajuda ai
Determinar o ângulo entre as seguintes retas:


-
mayconf
- Usuário Dedicado

-
- Mensagens: 28
- Registrado em: Sex Set 21, 2012 12:11
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por young_jedi » Seg Set 24, 2012 15:05
por young_jedi » Seg Set 24, 2012 15:05
prieiro colocar na forma parametrica as duas retas
em seguida encontrar o vetor diretor de cada reta e pelo produto escalar entre eles encontrar o angulo
para colocar na forma parametrica r1

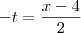
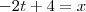
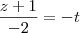
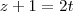
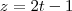
r1:
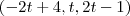
r1:
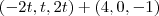
r1:

sendo assim seu vetor direção é (-2,1,2)
faça o mesmo para r2 e deois use o produto escalar
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por mayconf » Seg Set 24, 2012 17:50
por mayconf » Seg Set 24, 2012 17:50
na r2, o y é igual a t também? se for vai dar fração certo?
-
mayconf
- Usuário Dedicado

-
- Mensagens: 28
- Registrado em: Sex Set 21, 2012 12:11
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por young_jedi » Seg Set 24, 2012 19:35
por young_jedi » Seg Set 24, 2012 19:35
Vai, mas não tem problema algum
pode fazer que vai dar certo
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por mayconf » Ter Set 25, 2012 12:26
por mayconf » Ter Set 25, 2012 12:26
brigadão ae young_jedi
-
mayconf
- Usuário Dedicado

-
- Mensagens: 28
- Registrado em: Sex Set 21, 2012 12:11
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
Voltar para Álgebra Linear
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Ângulo entre retas
por Claudin » Seg Jul 16, 2012 03:22
- 4 Respostas
- 2658 Exibições
- Última mensagem por Claudin

Seg Jul 16, 2012 04:19
Geometria Analítica
-
- Angulo entre retas
por LucasSG » Seg Jun 10, 2013 21:16
- 1 Respostas
- 2445 Exibições
- Última mensagem por young_jedi

Ter Jun 11, 2013 19:13
Geometria Analítica
-
- Ângulo entre duas retas
por Jonatan » Qui Jul 22, 2010 13:38
- 0 Respostas
- 3585 Exibições
- Última mensagem por Jonatan

Qui Jul 22, 2010 13:38
Geometria Analítica
-
- Angulo Entre Duas Retas
por mayconf » Sex Set 21, 2012 13:33
- 2 Respostas
- 17736 Exibições
- Última mensagem por mayconf

Sex Set 21, 2012 18:09
Geometria Analítica
-
- Angulo entre retas {vetores}
por Danilo » Ter Nov 06, 2012 16:07
- 3 Respostas
- 3061 Exibições
- Última mensagem por young_jedi

Qui Nov 08, 2012 10:20
Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.







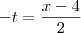
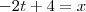
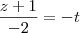
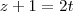
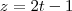
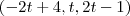
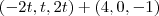





 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.