RenatoP escreveu:Olá, não consegui desenvolver nada na verdade...
Não entendi, mesmo pq o boldrini não explica no livro, o que seriam essas duas funções na integral, e o que eu faço com as informações que ele passou.
Eu deveria desenvolver as funções como polinomios de segundo grau, p(t) = at² + bt + c ?
Ficou muito vaga a explicação no livro dele (e no Steinbruch tbm)...
Vejamos a "tradução" de cada parte do enunciado do exercício.
RenatoP escreveu:Seja P2 o espaço das funções polinomiais reais de grau menor ou igual a dois.
Ou seja, o espaço P2 é formado por funções do tipo f(t) = c, g(t) = bt + c ou h(t) = at² + bx + c.
RenatoP escreveu:Considere a função:
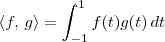
Temos uma função, representada por "<, >", que pega duas funções f e g no espaço P2 e associa com o valor de
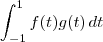
.
Por exemplo, se f(t) = t + 1 e g(t) = t², então:
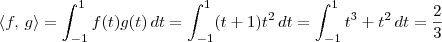
RenatoP escreveu:Considere W o subespaço de P2 gerado pelos vetores p(t) = 1 e q(t) = 1-t
Como W é subespaço de P2, isso significa que W é um subconjunto de P2 com as seguintes propriedades:
(i) a função f(t) = 0 pertence a W;
(ii) se f(t) e g(t) pertencem a W, então f(t) + g(t) também pertence a W;
(iii) se f(t) pertence a W e k é um escalar qualquer, então kf(t) também pertence a W.
Além disso, como W é gerado por p(t) = 1 e q(t) = 1 - t, se f(t) pertence a W, então existem escalares a e b tais que f(t) = ap(t) + bq(t). Em outras palavras, todos os elementos de W podem ser escritos como uma combinação linear de p(t) e q(t).
RenatoP escreveu:a) <f, g> é um produto interno?
Para responder essa pergunta você precisa verificar as quatro propriedades que definem o produto interno:
(i)
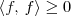
, para toda f em P2;
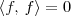
se, e somente se, f = 0.
(ii)
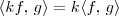
, para todo escalar k;
(iii)
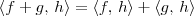
;
(iv)
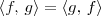
.
Eu vou verificar a primeira propriedade e você tenta as outras três.
Verificação da propriedade i)Aplicando a definição da função <, >, temos que:
![\langle f,\,f\rangle = \int_{-1}^{1}f(t)f(t)\,dt = \int_{-1}^{1}[f(t)]^2\,dt \langle f,\,f\rangle = \int_{-1}^{1}f(t)f(t)\,dt = \int_{-1}^{1}[f(t)]^2\,dt](/latexrender/pictures/afa93619f4c53cee2d5cfd483f8e5e23.png)
Das propriedades de integral, sabemos que se
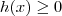
, então
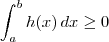
.
Sendo assim, como
![[f(t)]^2 \geq 0 [f(t)]^2 \geq 0](/latexrender/pictures/183c201552590ac049bba5bfb58037cb.png)
, temos que
![\int_{-1}^{1}[f(t)]^2\,dt \geq 0 \int_{-1}^{1}[f(t)]^2\,dt \geq 0](/latexrender/pictures/ba4ed95bd5200561af326baff6bea1f8.png)
.
Ou seja, concluímos que
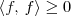
.
Suponha agora que
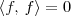
Sabemos que o formato geral de uma função f em P2 é f(t) = at² + bt + c. Desse modo, temos que:
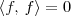
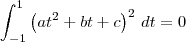
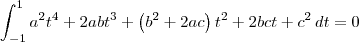
![\left[\frac{a^2}{5}t^5 + \frac{ab}{2}t^4 + \frac{\left(b^2+2ac\right)}{3}t^3 + bct^2 + c^2t\right]_{-1}^{1} = 0 \left[\frac{a^2}{5}t^5 + \frac{ab}{2}t^4 + \frac{\left(b^2+2ac\right)}{3}t^3 + bct^2 + c^2t\right]_{-1}^{1} = 0](/latexrender/pictures/a83da0ea7f42f8b54ba9a8dbb09b7e69.png)
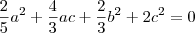
Enxergando essa equação como uma equação polinomial do 2° grau na incógnita a, então temos que:
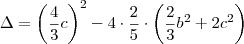
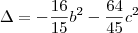
Se b ou c fossem diferentes de 0, então teríamos b² > 0 ou c² > 0. Nesse caso, iria ocorrer
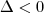
e portanto não haveria solução real para a equação dada.
Por outro lado, se b = c = 0, então

e a solução da equação seria a = 0.
Disso concluímos que a única solução é a = b = c = 0. Ou seja, temos que f(t) = 0.
Em resumo, verificamos que se
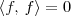
, então temos

.
Vamos agora verificar o contrário. Suponha que f(t) = 0. Temos que:
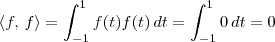
Ou seja, se

, então
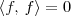
.
Unindo essas informações, podemos dizer que
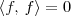
se, e somente se, f = 0.
Isso completa a verificação da propriedade i).
Agora basta você verificar as outras propriedades. A boa notícia é: as verificações serão bem menos trabalhosas do que a que fizemos para a propriedade i). Elas usarão apenas propriedades das integrais.
RenatoP escreveu:b) Se a) for afirmativa, determine uma base ortogonal para W.
Após verificar que as quatro propriedades anteriores são válidas, você poderá dizer que a afirmativa a) é verdadeira. Isto é, dizer que <f, g> é um produto interno.
Lembrando então que W é gerado por p(t) = 1 e q(t) = 1 - t, e notando que p(t) e q(t) são linearmente independentes, podemos dizer que {p, q} é uma base de W.
Entretanto, essa base não é ortogonal, pois se calcularmos <p, q> não obtemos 0. Apesar disso, podemos obter uma base ortogonal a partir dela. Para isso, basta aplicar o
Processo de Ortogonalização de Gram-Schmidt.
Tente aplicar esse processo para obter uma base ortogonal.
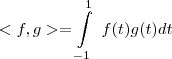
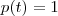 e
e 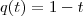


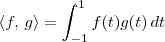

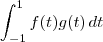 .
.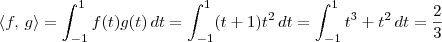
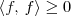 , para toda f em P2;
, para toda f em P2; 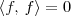 se, e somente se, f = 0.
se, e somente se, f = 0.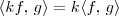 , para todo escalar k;
, para todo escalar k;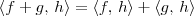 ;
;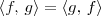 .
.![\langle f,\,f\rangle = \int_{-1}^{1}f(t)f(t)\,dt = \int_{-1}^{1}[f(t)]^2\,dt \langle f,\,f\rangle = \int_{-1}^{1}f(t)f(t)\,dt = \int_{-1}^{1}[f(t)]^2\,dt](/latexrender/pictures/afa93619f4c53cee2d5cfd483f8e5e23.png)
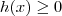 , então
, então 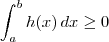 .
.![[f(t)]^2 \geq 0 [f(t)]^2 \geq 0](/latexrender/pictures/183c201552590ac049bba5bfb58037cb.png) , temos que
, temos que ![\int_{-1}^{1}[f(t)]^2\,dt \geq 0 \int_{-1}^{1}[f(t)]^2\,dt \geq 0](/latexrender/pictures/ba4ed95bd5200561af326baff6bea1f8.png) .
.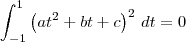
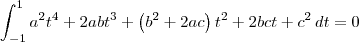
![\left[\frac{a^2}{5}t^5 + \frac{ab}{2}t^4 + \frac{\left(b^2+2ac\right)}{3}t^3 + bct^2 + c^2t\right]_{-1}^{1} = 0 \left[\frac{a^2}{5}t^5 + \frac{ab}{2}t^4 + \frac{\left(b^2+2ac\right)}{3}t^3 + bct^2 + c^2t\right]_{-1}^{1} = 0](/latexrender/pictures/a83da0ea7f42f8b54ba9a8dbb09b7e69.png)
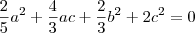
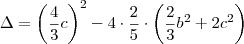
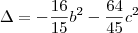
 e portanto não haveria solução real para a equação dada.
e portanto não haveria solução real para a equação dada. e a solução da equação seria a = 0.
e a solução da equação seria a = 0. .
.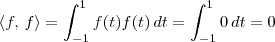
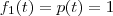

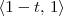 e
e 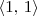 .
.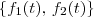 .
.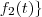 mas estava esquecendo de que a base era
mas estava esquecendo de que a base era 
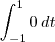
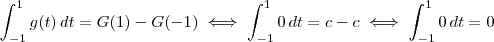
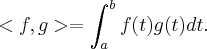
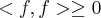 .
. . O que ela
. O que ela 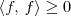 . Ou seja, não há uma "generalização" como você está tentando dizer.
. Ou seja, não há uma "generalização" como você está tentando dizer.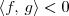 .
. .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
