Oi estou com uma extrema dificuldade em um tipo de exercicio de subespaços vetoriais. O problema maior é que estava acostmado a exercicios em que o enunciado ja fornecia a 'cara' do vetor. Vou colocar a questao e depois eu falo mais sobre minhas duvidas.
6. Determine se cada conjunto a seguir é ou não um subespaço de C[-1 , 1].
(a) O conjunto das funções f em C[-1 , 1] tais f (-1) = f (1).
(b) O conjunto das funções ímpares em C[-1 , 1].
(c) O conjunto das funções não decrescentes em [-1 , 1].
(d) O conjunto das funções em f em C [-1 , 1] tais f (-1) = 0 e f (1) = 0.
(e) O conjunto das funções f em C [-1 , 1] tais f (-1) = 0 ou f (1) = 0.
[Retirado de Algebra Linear com Aplicaçoes de Steven J. Leon]
1º : Nao sei o que quer dizer o "C" de "C[-1 , 1]".
2º : O que seria "O espaço das funçoes f".
3º : Bem se nao for pedir de mais, poderiam, por favor, fazer uma das letras.
Para mim, este é o melhor metodo de se aprender uma materia vendo exercicios resolvidos. Normalmente os professores só dao teoremas e exemplos tao mediocres que ao inves de ajudar o aluno apenas iludem, fazem parecer que é tudo simples. Pra isso tem o livro. Professor, na minha opiniao deveria usar a maior parte da aula resolvendo exercicios considerados dificeis e mostrando, se possivel, as aplicaçoes. Bem é o que eu acho, aluno bom vai pra aula com a materia ja estudada (ou ao menos lida).
Obrigado.


![C[-1,1] C[-1,1]](/latexrender/pictures/e9b30fbca78234398355a477ab607259.png) é o espaço das [b]funções contínuas no intervalo [-1,1][/tex]. Ou seja, você considera todas as funções com a característica de serem contínuas neste intervalo. Por último, vou fazer apenas a primeira pois as outras seguem da mesma forma (até mesmo para contra-exemplos).
é o espaço das [b]funções contínuas no intervalo [-1,1][/tex]. Ou seja, você considera todas as funções com a característica de serem contínuas neste intervalo. Por último, vou fazer apenas a primeira pois as outras seguem da mesma forma (até mesmo para contra-exemplos).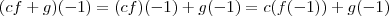 . Pela propriedade, sabemos que toda função desse subespaço tem sua avaliação igual em -1 e 1. Daí,
. Pela propriedade, sabemos que toda função desse subespaço tem sua avaliação igual em -1 e 1. Daí, 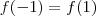 e
e 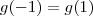 . Assim,
. Assim, 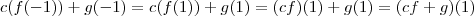 . Portanto, toda combinação linear de elementos pertence ao subespaço.
. Portanto, toda combinação linear de elementos pertence ao subespaço.

 não prova nada. Veja o correto:
não prova nada. Veja o correto:![W = \left\{ f \in C[-1,1] \; | \; f(-1) = f(1) \right\} W = \left\{ f \in C[-1,1] \; | \; f(-1) = f(1) \right\}](/latexrender/pictures/b2b3a121f461dc3c38a7b791686c34a2.png) . Tome
. Tome 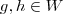 . Então
. Então 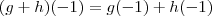 . Como estão em
. Como estão em  , teremos que
, teremos que 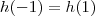 , logo
, logo 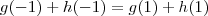 , daí
, daí 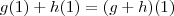 e portanto
e portanto 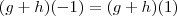 .
.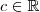 e
e 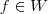 . Então
. Então 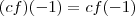 , como a função pertence a
, como a função pertence a 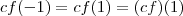 , portanto
, portanto 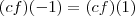 e isto prova que é subespaço.
e isto prova que é subespaço.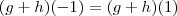 é assumir o que você quer provar, um erro fatal.
é assumir o que você quer provar, um erro fatal.