Olá Manoella,
Primeiro, não é porque você estuda Matemática que pode descuidar-se do Português. Portanto, veja as correções do colega como uma crítica construtiva e evite escrever errado, seja lá onde for.
Agora, vejamos a sua dúvida.
Vamos começar com noções intuitivas e não muito formais. Vamos pensar em funções de um modo geral (lembre-se que uma transformação linear é uma função, mas que tem duas propriedades particulares: preserva a soma; preserva o produto por escalar).
Considere dois conjuntos, A e B, de modo que A tem 3 elementos e B tem 2 elementos.
É possível criar uma função de A para B que seja injetora? Bem, sabemos que uma função é injetora quando para quaisquer dois elementos diferentes do domínio tivermos imagens diferentes, isto é, a associação entre domínio e imagem é de 1 para 1. Perceba que não é possível fazer isso nesse caso, pois no conjunto A sempre sobraria um elemento, o que não pode ocorrer já que A deveria ser o domínio da função. Veja o diagrama abaixo.
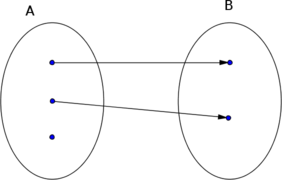
- Não pode haver função injetora de A para B.
- Diagrama1.png (19.96 KiB) Exibido 8198 vezes
Por outro lado, é possível criar uma função de B para A que seja sobrejetora? Bem, sabemos que uma função é sobrejetora quando o contra-domínio é igual a imagem, isto é, todo elemento do contra-domínio está associado a algum elemento do domínio. Perceba que não é possível fazer isso nesse caso, pois no conjunto B haveria um elemento associado a mais de um elemento do conjunto A, o que não pode ocorrer já que B deveria ser o domínio da função. Veja o diagrama abaixo.
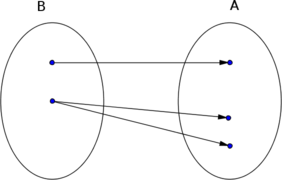
- Não pode haver função sobrejetora de B para A.
- Diagrama2.png (21.34 KiB) Exibido 8198 vezes
Dito isso, vamos analisar as transformações lineares de
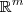
em

. Nos exemplos anteriores, os conjuntos A e B eram finitos, entretanto agora estamos tratando com dois conjuntos infinitos. Porém, se m>n, os conjuntos
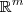
e

possuem dimensões distintas e haverá "mais elementos" em
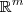
do que em

(apesar dos dois conjuntos serem infinitos). Utilizando as noções vistas anteriormente, poderemos então enxergar intuitivamente a afirmação:
Se m>n, então:
(i) a transformação linear

não pode ser injetora.
(ii) a transformação linear
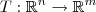
não pode ser sobrejetora.
Observação: Para entender melhor sobre essa ideia de dois conjuntos infinitos, mas que um tem "mais elementos" do que outro, você precisa estudar Teoria de Conjuntos, principalmente o conceito de cardinalidade. Apenas como outro exemplo, os conjuntos
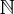
,

e

possuem a mesma cardinalidade, mas o conjunto

tem uma cardinalidade maior do que qualquer um desses conjuntos. Ou seja, é correto afirmar que há mais números reais do que naturais, inteiros ou racionais, apesar de todos esses conjuntos serem infinitos.
Agora, sendo um pouco mais formal, há um teorema que é muito aplicado para discutir sobre injetividade e sobrejetividade de transformações lineares. Trata-se do
Teorema da Dimensão do Núcleo e da Imagem:
Seja

uma transformação linear, então é válido que:
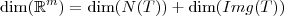
,
onde N(T) é o núcleo da transformação linear e Img(T) é a sua imagem.
Usando esse teorema, vejamos como justificar as afirmações (i) e (ii):
Se m>n, então:
(i) a transformação linear

não pode ser injetora.
Se T fosse injetora, então
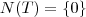
e por definição
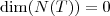
. Usando o teorema, deveríamos ter:
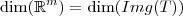
,
porém
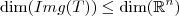
, de onde teríamos:

Mas, isso é absurdo, já que por hipótese m>n. Portanto, T não pode ser injetora.
ii) a transformação linear
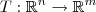
não pode ser sobrejetora.
Se T fosse sobrejetora, então
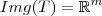
e portanto
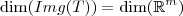
. Usando o teorema, deveríamos ter:
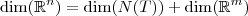
,
de onde teríamos:
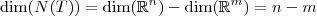
Mas, isso é absurdo, já que por hipótese m>n e desse modo teríamos

, o que não pode ocorrer já que não há dimensão negativa. Portanto, T não pode ser sobrejetora.
Por fim, recomendo que você estude cuidadosamente esses conceitos. Se desejar, use o livro "Introdução à Álgebra Linear" de Reginaldo J. Santos, disponível em:
http://www.mat.ufmg.br/~regi/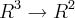 ? existe sim...Mas pq??? Mim ajude a explicar com calculos?
? existe sim...Mas pq??? Mim ajude a explicar com calculos?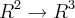 . Mim ajude a fazer os calculos do Pq, disso?
. Mim ajude a fazer os calculos do Pq, disso?


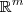 em
em  . Nos exemplos anteriores, os conjuntos A e B eram finitos, entretanto agora estamos tratando com dois conjuntos infinitos. Porém, se m>n, os conjuntos
. Nos exemplos anteriores, os conjuntos A e B eram finitos, entretanto agora estamos tratando com dois conjuntos infinitos. Porém, se m>n, os conjuntos  não pode ser injetora.
não pode ser injetora.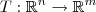 não pode ser sobrejetora.
não pode ser sobrejetora. ,
,  e
e  possuem a mesma cardinalidade, mas o conjunto
possuem a mesma cardinalidade, mas o conjunto  tem uma cardinalidade maior do que qualquer um desses conjuntos. Ou seja, é correto afirmar que há mais números reais do que naturais, inteiros ou racionais, apesar de todos esses conjuntos serem infinitos.
tem uma cardinalidade maior do que qualquer um desses conjuntos. Ou seja, é correto afirmar que há mais números reais do que naturais, inteiros ou racionais, apesar de todos esses conjuntos serem infinitos.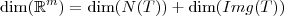 ,
, e por definição
e por definição 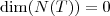 . Usando o teorema, deveríamos ter:
. Usando o teorema, deveríamos ter: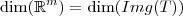 ,
,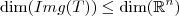 , de onde teríamos:
, de onde teríamos:
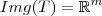 e portanto
e portanto 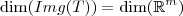 . Usando o teorema, deveríamos ter:
. Usando o teorema, deveríamos ter: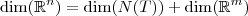 ,
,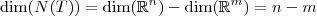
 , o que não pode ocorrer já que não há dimensão negativa. Portanto, T não pode ser sobrejetora.
, o que não pode ocorrer já que não há dimensão negativa. Portanto, T não pode ser sobrejetora.