 por jlr2906 » Sáb Set 01, 2018 05:03
por jlr2906 » Sáb Set 01, 2018 05:03
Se det(A + B) é DIFERENTE de 0 então A ou B são invertíveis.
Vdd ou falso e demonstrar ou justificar o pq, pf?
-
jlr2906
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Sáb Set 01, 2018 04:55
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Alimentos
- Andamento: cursando
 por adauto martins » Sex Mai 01, 2020 19:04
por adauto martins » Sex Mai 01, 2020 19:04
as matrizes A e B quadradas(pois,calcularemos seu determinante) e de mesma ordem...

onde M,quadrade e mesma ordem de A e B,
e I(matriz identidade)
como as matrizes A,B,M sao quadradas e de mesma ordem,
vale a propriedade associativa(MOSTRE ISSO),a saber
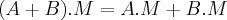
logo nao podemos ter A e B ambas invertiveis,pois
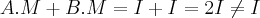
...
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
Voltar para Álgebra Linear
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Logica - Se A então B.
por Moura » Seg Abr 01, 2013 11:04
- 0 Respostas
- 1243 Exibições
- Última mensagem por Moura

Seg Abr 01, 2013 11:04
Lógica
-
- matrizes invertiveis
por kath » Sex Abr 18, 2014 02:32
- 1 Respostas
- 3332 Exibições
- Última mensagem por e8group

Sex Abr 18, 2014 15:53
Matrizes e Determinantes
-
- resultado diferente - PG
por jose henrique » Qui Set 30, 2010 23:50
- 4 Respostas
- 3208 Exibições
- Última mensagem por MarceloFantini

Ter Out 05, 2010 01:18
Progressões
-
- Regra de 3 diferente
por c_zaidan » Qua Dez 08, 2010 17:51
- 2 Respostas
- 3459 Exibições
- Última mensagem por c_zaidan

Qua Dez 08, 2010 19:46
Álgebra Elementar
-
- [Limite]de sen(x)/x = 1 só se x diferente de ...
por marcosmuscul » Qui Mar 28, 2013 20:34
- 3 Respostas
- 2854 Exibições
- Última mensagem por marcosmuscul

Sex Mar 29, 2013 14:00
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.




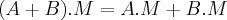
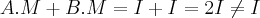 ...
...