 por fernando7 » Qua Abr 11, 2018 20:46
por fernando7 » Qua Abr 11, 2018 20:46
Tentei fazer os exercícios mais estou com muita duvidas não sei ser as respostas estão corretas.
https://ibb.co/dhU5Px 
-
fernando7
- Usuário Ativo

-
- Mensagens: 14
- Registrado em: Qua Abr 11, 2018 20:31
- Formação Escolar: ENSINO FUNDAMENTAL II
- Andamento: cursando
 por Gebe » Qui Abr 12, 2018 01:05
por Gebe » Qui Abr 12, 2018 01:05
Tem alguns erros. Vou resolver as questões 2 e 3. Ja na 4, não consegui identificar o vetor "d" no desenho e também não ha qualquer mençao sobre ele, portanto fica dificil calcular o trabalho.
2a)
Esta questão está correta.
2b)
Aqui teu erro foi ter feito a subtração antes da multiplicação do vetor u' pelo escalar 2. O certo fica:

2c)
Aqui temos um produto escalar de dois vetores, representado pelo "ponto". O produto escalar de dois vetores tem como resultado um escalar (um numero), não um vetor.
ex.:
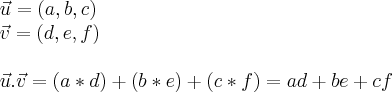
Logo:
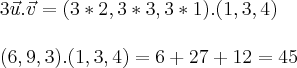
3)
Esta precisa um pouco mais de atenção. Primeiramente na equação do trabalho "F" e "d" sem o simbolo de vetor (flecha) significa que estamos trabalhando com o modulo deste vetor, logo a equação é na verdade

. Perceba também que nesta equação precisamos do cosseno do angulo entre os dois vetores.
Vamos então fazer por partes:
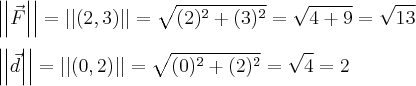 https://ibb.co/n5zYSH
https://ibb.co/n5zYSHComo podemos ver pela representação dos dois vetores temos cateto op igual a 2, adj igual a 3 e hip igual a Raiz(13).
Portanto:
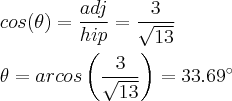

4)
Força resltante:
Eixo y = F1 - F3 + F2y = 4 - 1 + 2sen(30°) = 3+1= 4
Eixo x = F2x = 2cos(30°) = Raiz(3)
Força resultante = Raiz(3) i + 4j
Angulo com a vertical (eixo y) = arctg ( cat oposto / cat adj ) = arcos ( Raiz(3) / 4 ) = 23.41°
Espero ter ajudado, qualquer duvida mande msg
Editado pela última vez por
Gebe em Sex Abr 13, 2018 03:36, em um total de 1 vez.
-
Gebe
- Colaborador Voluntário

-
- Mensagens: 158
- Registrado em: Qua Jun 03, 2015 22:47
- Formação Escolar: GRADUAÇÃO
- Área/Curso: engenharia eletrica
- Andamento: cursando
 por fernando7 » Qui Abr 12, 2018 03:33
por fernando7 » Qui Abr 12, 2018 03:33
Questão 2
Faltou as regras básicas:
1° * e /
2° + e -
Questão 4
d(2,0) não poderia ser o vetor d?
Na questão 3 usei o arctg (cat. op. / cat. adj. ) foi passado pelo professor.
arctg => 3,01/2=1,505 => 56,40°
-
fernando7
- Usuário Ativo

-
- Mensagens: 14
- Registrado em: Qua Abr 11, 2018 20:31
- Formação Escolar: ENSINO FUNDAMENTAL II
- Andamento: cursando
 por Gebe » Qui Abr 12, 2018 15:38
por Gebe » Qui Abr 12, 2018 15:38
As regras basicas são simples, a soma e subtração, por exemplo, tu havias feito certo, teu erro foi quanto a ordem das operações. Na "b" tu primeiro fez a subtração e depois fez o produto por escalar, quando deverias primeiro ter feito o produto escalar.
As operações de produto e divisao exigem um pousoc mais de atenção. O produto pode ter 3 tipos:
- Produto de um vetor por um escalar (numero). ex.: 3u' onde u' é um vetor.
- Produto escalar entre dois vetores. Este tem como resultado um numero. O simbolo desta operação é um ponto.
- Produto vetorial entre dois vetores. Este tem como resultado outro vetor. O simbolo desta operação é um "x".
Os dois primeiros tipos foram citados e mostrados durante a resolução que passei. O terceiro tipo (prod vetorial) é possivel que tu nao tenhas visto ainda e, como não foi utilizado nas questoes, não vou falar sobre. Caso tenha duvidas ainda sobre os dois primeiros ou queira saber mais sobre o prod. vetorial é só mandar uma msg.
A divisão pode ser feita APENAS de um vetor por um escalar (numero). ex.: u'/2 onde u' é um vetor qualquer. Não existe divisão entre dois vetores.
Sobre o vetor deslocamento na questão 4. As questões são diferentes, a não ser que tenha sido dito pra considerar este vetor nas duas questões.
No entanto, caso seja, ficaria:
W = ||d|| . ||Fr|| . cos (63.67°)
W = ||(0,2)|| . 3.905 . ( Raiz(3) / 3.905 )
W = 2 . 3.905 . ( Raiz(3) / 3.905 )
W = 2.Raiz(3)
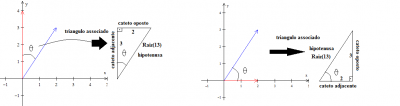
Sobre a questão 3. Pode usar arcos, arcsen ou arctg. Qualquer um resultaria no mesmo angulo. O erro foi quanto ao valor que tu atribuiu aos catetos e hip. Lembre-se que o cateto oposto é o lado do triangulo oposto ao angulo feito pelos dois vetores (veja no desenho que eu coloquei). A hip é o lado maio, ou se preferir, o lado oposto ao angulo de 90° do triangulo. Por ultimo o cateto adj é o lado mais "proximo" ao angulo entre os dois vetores.
Seguindo essa logica teremos:
-> cateto oposto = 2
-> cateto adj = 3
-> hip = Raiz(13)
Sendo assim o angulo entre os vetores poderia ser calculado por:
->Arcsen ( 2 / raiz(13) ) = 33.69°
-> Arcos ( 3 / Raiz(13) ) = 33.69°
-> Arctg ( 2 / 3 ) = 33.69°
Para conferir basta colocar na calculadora.
O que tu fez na verdade foi calcular o angulo entre o eixo "x" e o vetor Força.
Se permanecerem duvidas é só mandar msg.
-
Gebe
- Colaborador Voluntário

-
- Mensagens: 158
- Registrado em: Qua Jun 03, 2015 22:47
- Formação Escolar: GRADUAÇÃO
- Área/Curso: engenharia eletrica
- Andamento: cursando
 por fernando7 » Sex Abr 13, 2018 01:05
por fernando7 » Sex Abr 13, 2018 01:05
Questão 3 e 4 esta osso.
Na questão 3 achei o cos de 56,40° e 3,99J
hip = 3,605551275 = 3,61
cat op
(3,61)² = (2)²+b²
13,0321=4+b²
b²=9,0321
b=3,005345238 => 3,01
Ângulo = 3,01/2=1,505 => 56,39787681° => 56,40°
cat adj = 2
w=1,73205080757 X 2 X 0,553391549243
w= 3,99 J
Questão 4 não entendi nada.
-
fernando7
- Usuário Ativo

-
- Mensagens: 14
- Registrado em: Qua Abr 11, 2018 20:31
- Formação Escolar: ENSINO FUNDAMENTAL II
- Andamento: cursando
 por Gebe » Sex Abr 13, 2018 03:36
por Gebe » Sex Abr 13, 2018 03:36
Novamente, o erro na tua resolução não é quanto as contas, mas sim quanto a identificação dos catetos.
Se tu troca o oposto pelo adjacente o angulo também vai mudar.
É essencial que tu desenhe o plano cartesiano e os vetores nele para que assim tu possa identificar corretamente os catetos.
A figura que eu postei em uma das msgs anteriores exemplifica este desenho, porem vou colocar mais um em anexo.
Perceba que inclusive tu estas calculando o cateto oposto, no entanto nao é necessario, pois ja temos o seu valor que é 3.
A hipotenusa pode ser calculada por pitagoras ou basta lembrar olhando pra figura que ela tem o mesmo tamanho do vetor (modulo do vetor).
A questão 4 precisa que seja primeiro calculado o vetor força resultante.
-> Temos 3 forças, duas são verticais ( F1 e F3) e outra faz 30° com a horizontal (F2).
-> A força F2 pode ser decomposta em duas forças, uma horizontal ( F2cos(30°) ) e outra vertical ( F2sen(30°) ).
-> Somando as componentes verticais temos: F1 + F3 + F2sen(30°) = 4 + (-1) + 2sen(30°) = 3 + 1 = 4
-> Somando as componentes horizontais temos: F2cos(30°) = 2* ( Raiz(3) / 2 ) = Raiz(3)
-> Vetor Fr fica então:
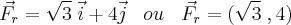
-> Pra calcular o trabalho precisamos do vetor deslocamento que, como discutido anteriormente, nao foi dado.
- Anexos
-
-
Gebe
- Colaborador Voluntário

-
- Mensagens: 158
- Registrado em: Qua Jun 03, 2015 22:47
- Formação Escolar: GRADUAÇÃO
- Área/Curso: engenharia eletrica
- Andamento: cursando
Voltar para Álgebra Linear
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Ângulo/circunferência] Ângulo CÂB, ajude-me!
 por miltonsermoud » Qua Set 30, 2015 17:14
por miltonsermoud » Qua Set 30, 2015 17:14
- 3 Respostas
- 3503 Exibições
- Última mensagem por miltonsermoud

Sex Out 02, 2015 07:41
Geometria Plana
-
- angulo
por cristina » Qua Set 23, 2009 00:08
- 4 Respostas
- 2795 Exibições
- Última mensagem por cristina

Ter Set 29, 2009 11:28
Trigonometria
-
- Ângulo
por Balanar » Seg Ago 30, 2010 20:24
- 1 Respostas
- 2444 Exibições
- Última mensagem por Molina

Seg Ago 30, 2010 23:28
Geometria Plana
-
- Angulo
por Thays » Ter Jan 17, 2012 14:21
- 1 Respostas
- 1691 Exibições
- Última mensagem por Arkanus Darondra

Ter Jan 17, 2012 14:37
Sistemas de Equações
-
- Angulo
por Thays » Sex Jan 27, 2012 10:49
- 1 Respostas
- 1769 Exibições
- Última mensagem por Molina

Sex Jan 27, 2012 13:47
Sistemas de Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
método de contagem
Autor:
sinuca147 - Seg Mai 25, 2009 09:10
Veja este exercício:
Se A = {

} e B = {

}, então o número de elementos A

B é:
Eu tentei resolver este exercício e achei a resposta "três", mas surgiram muitas dúvidas aqui durante a resolução.
Para determinar os elementos do conjunto A, eu tive de basicamente fazer um lista de vinte dividido por todos os números naturais maiores que zero e menores que vinte e um, finalmente identificando como elementos do conjunto A os números 1, 2, 4, 5, 10 e 20. Acho que procedi de maneira correta, mas fiquei pensando aqui se não existiria um método mais "sofisticado" e prático para que eu pudesse identificar ou ao menos contar o número de elementos do conjunto A, existe?
No processo de determinação dos elementos do conjunto B o que achei foi basicamente os múltiplos de cinco e seus opostos, daí me surgiram estas dúvidas:
existe oposto de zero?
existe inverso de zero?
zero é par, certo?
sendo x um número natural, -x é múltiplo de x?
sendo z um número inteiro negativo, z é múltiplo de z?
sendo z um número inteiro negativo, -z é múltiplo de z?
A resposta é 3?
Obrigado.
Assunto:
método de contagem
Autor:
Molina - Seg Mai 25, 2009 20:42
Boa noite, sinuca.
Se A = {

} você concorda que n só pode ser de 1 a 20? Já que pertence aos naturais?
Ou seja, quais são os divisores de 20? Eles são seis: 1, 2, 4, 5, 10 e 20.
Logo, o conjunto A é
A = {1, 2, 4, 5, 10, 20}
Se B = {

} você concorda que x será os múltiplos de 5 (positivos e negativos)? Já que m pertence ao conjunto Z?
Logo, o conjunto B é
B = {... , -25, -20, -15, -10, -5, 0, 5, 10, 15, 20, 25, ...
Feito isso precisamos ver os números que está em ambos os conjuntos, que são:
5, 10 e 20 (3 valores, como você achou).
Vou responder rapidamente suas dúvidas porque meu tempo está estourando. Qualquer dúvida, coloque aqui, ok?
sinuca147 escreveu:No processo de determinação dos elementos do conjunto B o que achei foi basicamente os múltiplos de cinco e seus opostos, daí me surgiram estas dúvidas:
existe oposto de zero? sim, é o próprio zero
existe inverso de zero? não, pois não há nenhum número que multiplicado por zero resulte em 1
zero é par, certo? sim, pois pode ser escrito da forma de 2n, onde n pertence aos inteiros
sendo x um número natural, -x é múltiplo de x? Sim, pois basta pegar x e multiplicar por -1 que encontramos -x
sendo z um número inteiro negativo, z é múltiplo de z? Sim, tais perguntando se todo número é multiplo de si mesmo
sendo z um número inteiro negativo, -z é múltiplo de z? Sim, pois basta pegar -z e multiplicar por -1 que encontramos x
A resposta é 3? Sim, pelo menos foi o que vimos a cima
Bom estudo,

Assunto:
método de contagem
Autor:
sinuca147 - Seg Mai 25, 2009 23:35
Obrigado, mas olha só este link
http://www.colegioweb.com.br/matematica ... ro-natural
neste link encontra-se a a frase:
Múltiplo de um número natural é qualquer número que possa ser obtido multiplicando o número natural por 0, 1, 2, 3, 4, 5, etc.
Para determinarmos os múltiplos de 15, por exemplo, devemos multiplicá-lo pela sucessão dos números naturais:
Ou seja, de acordo com este link -5 não poderia ser múltiplo de 5, assim como 5 não poderia ser múltiplo de -5, eu sempre achei que não interessava o sinal na questão dos múltiplos, assim como você me confirmou, mas e essa informação contrária deste site, tem alguma credibilidade?
Há e claro, a coisa mais bacana você esqueceu, quero saber se existe algum método de contagem diferente do manual neste caso:
Para determinar os elementos do conjunto A, eu tive de basicamente fazer um lista de vinte dividido por todos os números naturais maiores que zero e menores que vinte e um, finalmente identificando como elementos do conjunto A os números 1, 2, 4, 5, 10 e 20. Acho que procedi de maneira correta, mas fiquei pensando aqui se não existiria um método mais "sofisticado" e prático para que eu pudesse identificar ou ao menos contar o número de elementos do conjunto A, existe?
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.





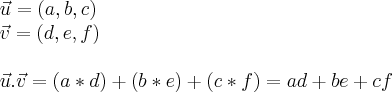
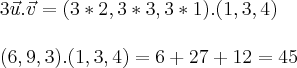
 . Perceba também que nesta equação precisamos do cosseno do angulo entre os dois vetores.
. Perceba também que nesta equação precisamos do cosseno do angulo entre os dois vetores.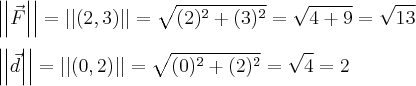
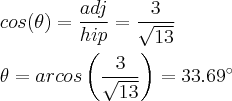





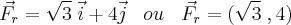

 } e B = {
} e B = { }, então o número de elementos A
}, então o número de elementos A  B é:
B é: } você concorda que n só pode ser de 1 a 20? Já que pertence aos naturais?
} você concorda que n só pode ser de 1 a 20? Já que pertence aos naturais? } você concorda que x será os múltiplos de 5 (positivos e negativos)? Já que m pertence ao conjunto Z?
} você concorda que x será os múltiplos de 5 (positivos e negativos)? Já que m pertence ao conjunto Z?