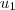 = (2,-1),
= (2,-1), 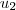 =(1,1)
=(1,1)  = (-1,-1),
= (-1,-1), 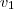 =(1,3),
=(1,3),  =(2,3) e
=(2,3) e 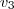 = (-5,-6). Decida se existe ou não um operador linear A:
= (-5,-6). Decida se existe ou não um operador linear A: 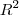 ?
?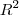 tal que
tal que 
Eu fiz, mas não sei se tá certo, fiz assim
a*(2,-1) + b*(1,1) + c*(-1,-1) = (x,y)
Montei o sistema e encontrei b-c=
 e a=
e a= 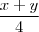
Depois fiz transformação
a*A
 + b-c*A
+ b-c*A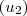
e obtive esse vetor w =
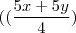 ,
, 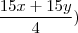
a minha dúvida é se meu raciocínio está correto e, se tiver, o que posso concluir disso? Eu acabei obtendo um r2 em r2, então quer dizer que é operador linear?


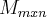 sempre determina uma transformaçao
sempre determina uma transformaçao 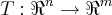 ,assim como uma transformaçao linear T e determinada por uma matriz
,assim como uma transformaçao linear T e determinada por uma matriz 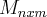 (prove isso)...
(prove isso)...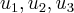 sao LI,e formam uma base p/
sao LI,e formam uma base p/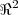 ,assim como
,assim como 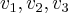 formam uma base p/
formam uma base p/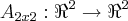 tal q. as sentenças sao verdadeiras...se caso positivo,encontre tal transformaçao...
tal q. as sentenças sao verdadeiras...se caso positivo,encontre tal transformaçao...

 .
.
 :
: