 por judsonpraxedes » Sex Dez 04, 2015 09:00
por judsonpraxedes » Sex Dez 04, 2015 09:00
Bom dia
Não estou conseguindo resolver a questão 25 do livro "Álgebra Linear - Steinbruch",
o enunciado diz o seguinte:
Encontre uma transformação linear de T: R³--> R², cujo nucleo N(T):[(1,0,-1)]
-
judsonpraxedes
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Sex Dez 04, 2015 08:56
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Exatas
- Andamento: cursando
 por adauto martins » Dom Mar 27, 2016 11:32
por adauto martins » Dom Mar 27, 2016 11:32
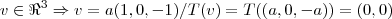
...como a DIM(I)=2teremos 2 equaçoes e tres incognitas,logo posso fazer a=x
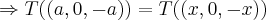
...p/qquer
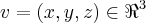
,podemos ter...
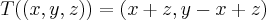
,pois x=-z,y=0 ou ainda
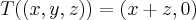
e etc...
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
Voltar para Álgebra Linear
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Transformação Linear] Nucleo e Imagem, ache a transformaçao
por vualas » Qua Nov 07, 2012 00:37
- 2 Respostas
- 4254 Exibições
- Última mensagem por adauto martins

Qui Dez 15, 2016 11:12
Álgebra Linear
-
- [Algebra Linear] - Composição de transformação Linear
por aligames321 » Ter Dez 04, 2012 23:53
- 1 Respostas
- 10533 Exibições
- Última mensagem por young_jedi

Qua Dez 05, 2012 12:45
Álgebra Linear
-
- Álgebra Linear -Transformação linear- Isomorfismo
por anapaulasql » Ter Jan 27, 2015 22:08
- 1 Respostas
- 11565 Exibições
- Última mensagem por adauto martins

Ter Mar 29, 2016 13:15
Álgebra Linear
-
- [Álgebra Linear] Transformação Linear Idenpotente
por Zubumafu67 » Ter Nov 17, 2020 11:38
- 0 Respostas
- 13607 Exibições
- Última mensagem por Zubumafu67

Ter Nov 17, 2020 11:38
Álgebra Linear
-
- [Álgebra Linear] Transformação linear
por Debby » Dom Mai 27, 2012 12:17
- 2 Respostas
- 9148 Exibições
- Última mensagem por Debby

Dom Mai 27, 2012 20:27
Álgebra Linear
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



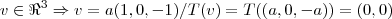 ...como a DIM(I)=2teremos 2 equaçoes e tres incognitas,logo posso fazer a=x
...como a DIM(I)=2teremos 2 equaçoes e tres incognitas,logo posso fazer a=x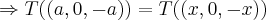 ...p/qquer
...p/qquer 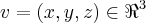 ,podemos ter...
,podemos ter...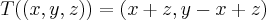 ,pois x=-z,y=0 ou ainda
,pois x=-z,y=0 ou ainda 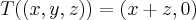 e etc...
e etc...

 .
.



