 por anapaulasql » Ter Jan 27, 2015 22:08
por anapaulasql » Ter Jan 27, 2015 22:08
Seja T:V-->W uma transformação linear injetora
i) Seja T:R³ --> R² definida por T(x,y,z)=(x+y+x, x-y+3z).
Encontre um subespaço V c R³ tal que a transformação linear definida por S: V --> R², S(x,y,z)= T(x,y,z)=(x+y+z, x-y+3z) seja injetora e sobrejetora.
-
anapaulasql
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Ter Jan 27, 2015 21:57
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia da Computação
- Andamento: cursando
 por adauto martins » Ter Mar 29, 2016 13:15
por adauto martins » Ter Mar 29, 2016 13:15
o nucleo de uma transformaçao linear é um subespaço da transformaçao(prove isso)...
logo
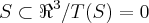
...
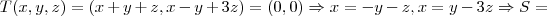
{
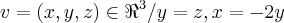
}...
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
Voltar para Álgebra Linear
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Algebra Linear] - Composição de transformação Linear
por aligames321 » Ter Dez 04, 2012 23:53
- 1 Respostas
- 10528 Exibições
- Última mensagem por young_jedi

Qua Dez 05, 2012 12:45
Álgebra Linear
-
- [Álgebra Linear] Transformação Linear Idenpotente
por Zubumafu67 » Ter Nov 17, 2020 11:38
- 0 Respostas
- 13602 Exibições
- Última mensagem por Zubumafu67

Ter Nov 17, 2020 11:38
Álgebra Linear
-
- [Álgebra Linear] Transformação linear
por Debby » Dom Mai 27, 2012 12:17
- 2 Respostas
- 9140 Exibições
- Última mensagem por Debby

Dom Mai 27, 2012 20:27
Álgebra Linear
-
- [Algebra Linear]-transformação linear
por Angel31 » Dom Out 28, 2012 10:10
- 1 Respostas
- 2970 Exibições
- Última mensagem por young_jedi

Dom Out 28, 2012 11:03
Álgebra Linear
-
- [Álgebra Linear ] Determine Uma matriz de transformação I de
por alienante » Seg Set 15, 2014 20:25
- 0 Respostas
- 2756 Exibições
- Última mensagem por alienante

Seg Set 15, 2014 20:25
Álgebra Linear
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


 ...
...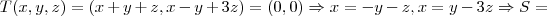 {
{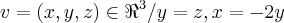 }...
}...
