o metodo e escalonar a matriz,tornando-a uma matriz triangular superior,de modo q. a diagonal fique somente numeros 1,
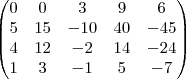
...podemos trocar linhas sem alterar a martriz,entao:
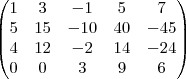
...agora e escalonar...com as operaçoes nas linhas da matriz,p/obter uma matriz triangular superior(livros de segundo grau,introduçao a algebra linear tem essas operaçoes)...
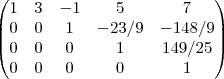
...como nao obtivemos a matriz com diagonal somente com 1,mas obtivemos matriz ,mais proxima possivel...
logo o sistema sera...
x+3y-z+5w=7,
z-(23/9)w=-148/9,
w=146/25...como a ultima linha dara 0=1,o sistema e incompativel,nao admite soluçao...
obs.:erro muito em contas numericas,entao convem refazer os calculo,mas o racicionio e esse...


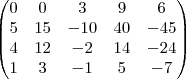 ...podemos trocar linhas sem alterar a martriz,entao:
...podemos trocar linhas sem alterar a martriz,entao: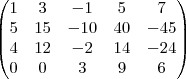 ...agora e escalonar...com as operaçoes nas linhas da matriz,p/obter uma matriz triangular superior(livros de segundo grau,introduçao a algebra linear tem essas operaçoes)...
...agora e escalonar...com as operaçoes nas linhas da matriz,p/obter uma matriz triangular superior(livros de segundo grau,introduçao a algebra linear tem essas operaçoes)...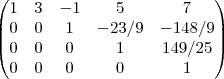 ...como nao obtivemos a matriz com diagonal somente com 1,mas obtivemos matriz ,mais proxima possivel...
...como nao obtivemos a matriz com diagonal somente com 1,mas obtivemos matriz ,mais proxima possivel...
 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
