
Minha humilde resolucao:





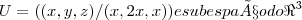 ;W=(1,0-1) e um ponto do {\Re}^{3}...
;W=(1,0-1) e um ponto do {\Re}^{3}...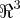 ,entao:
,entao: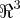 ,entao :U+W=(x+1,2x,x),
,entao :U+W=(x+1,2x,x),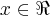
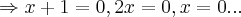 o q. contradiz pois x=-1 e x=0...logo U+W nao e subespaço do
o q. contradiz pois x=-1 e x=0...logo U+W nao e subespaço do 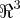

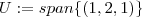 e pelo enunciado
e pelo enunciado 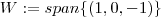 .
.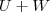 é subespaço do
é subespaço do 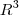 e assim um vetor arbitrário deste subespaço é
e assim um vetor arbitrário deste subespaço é 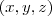 que se exprime como soma de dois vetores
que se exprime como soma de dois vetores 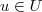 e
e  , e estes vetores são dados por
, e estes vetores são dados por 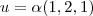 e
e  . Segue daí que
. Segue daí que 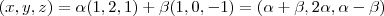 . Logo
. Logo 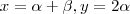 e
e 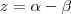 e por isso (soma x + z e substitui 2 alpha por y )
e por isso (soma x + z e substitui 2 alpha por y ) , pedro sua resposta está certa , porém confuso .
, pedro sua resposta está certa , porém confuso .

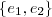 a base canônica para o
a base canônica para o 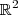 , de acordo com a notação acima
, de acordo com a notação acima ![\mathbb{R}^2 = [\{e_1 , e_2 \} ] \mathbb{R}^2 = [\{e_1 , e_2 \} ]](/latexrender/pictures/eab37dffaff4c2dc5911c50bdb67a424.png) .Eu particularmente evito esta notação e simplesmente escrevo
.Eu particularmente evito esta notação e simplesmente escrevo 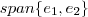 ou
ou 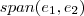 .
.
Usuários navegando neste fórum: Nenhum usuário registrado e 13 visitantes
 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.