 por dileivas » Qua Ago 07, 2013 20:53
por dileivas » Qua Ago 07, 2013 20:53
Estou com dificuldade em provar os 8 axiomas para mostrar que o conjunto de funções reais forma um espaço vetorial.
Minha primeira dúvida já começa na representação de uma função real. Estaria certo representar uma função real para essa prova como f(x) ou devo utilizar "n" variáveis do tipo f(x,y...,n)?
Minha segunda dúvida é em relação as operações de soma e multiplicação por escalar. Como ficariam?
Creio que sabendo isso consiga demonstrar os 8 axiomas.
Obrigado!
-
dileivas
- Usuário Ativo

-
- Mensagens: 15
- Registrado em: Qua Mar 14, 2012 20:54
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Ciências e Tecnologia / Engenharia
- Andamento: cursando
 por Russman » Qua Ago 07, 2013 21:36
por Russman » Qua Ago 07, 2013 21:36
Como "função real" você quer dizer o conjunto de funções contínuas do tipo
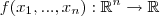
?
Se sim, para mostrar que é um espaço vetorial você deve mostrar que a soma e a multiplicação por um número real pertencem a esse espaço. Isto é verdade, pois a soma de duas funções reais contínuas é uma função real contínua assim como uma função real contínua multiplicada por um número real também é uma função real contínua.
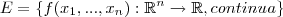
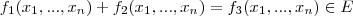
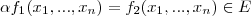
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por dileivas » Qua Ago 07, 2013 21:56
por dileivas » Qua Ago 07, 2013 21:56
Russman escreveu:Como "função real" você quer dizer o conjunto de funções contínuas do tipo
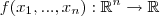
?
Creio que seja isso mesmo. Meu professor em aula deu exemplo de função real de uma variável f(x). Como o exercício pede a prova do "conjunto das funções reais" deve ser algo mais amplo como você indicou.
Aproveitando o tópico, no mesmo exercicio pede a prova do conjunto de matrizes 2x2 cujo o traço é zero. Como eu defino um vetor que está nesse conjunto? Seria algo do tipo
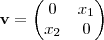
?
Muito obrigado pela ajuda!
-
dileivas
- Usuário Ativo

-
- Mensagens: 15
- Registrado em: Qua Mar 14, 2012 20:54
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Ciências e Tecnologia / Engenharia
- Andamento: cursando
 por Russman » Qui Ago 08, 2013 11:52
por Russman » Qui Ago 08, 2013 11:52
O traço de uma matriz é a soma dos elementos de sua diagonal. Assim, se
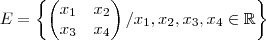
e tomarmos
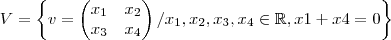
então, fazendo
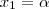
, temos
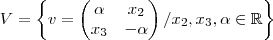
.
Se
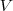
é espaço vetorial então para quaisquer
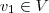
e
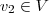
devemos verificar
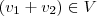
,
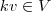
e a existência do elemento neutro.
De fato, o elemento neutro existe pois basta tomar
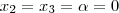
. Ainda,
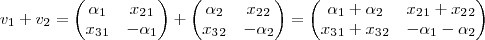
e como
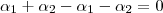
então
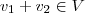
.
Agora,
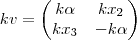
de modo que
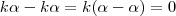
e, portanto,
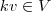
.
Assim,
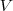
é espaço vetorial!
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por e8group » Qui Ago 08, 2013 16:15
por e8group » Qui Ago 08, 2013 16:15
Boa tarde . Observe a pagina 7 , exemplo 5 no seguinte link :
http://www.mat.ufmg.br/~regi/gaalt/gaalt2.pdf .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por BRUNA AVILA » Ter Ago 13, 2013 15:16
por BRUNA AVILA » Ter Ago 13, 2013 15:16
[color=#FF0000]Boa tarde!!
não consigo resolver o exercício de função inversa
Ache a função inversa 2x-1/3,minha dificuldade e porque não consigo resolver a fração,alguém pode me ajudar.[/color]
-
BRUNA AVILA
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Ter Ago 13, 2013 14:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em quimica
- Andamento: cursando
Voltar para Álgebra Linear
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- zeros reais de funções reais
por bebelo32 » Dom Mar 11, 2018 21:12
- 2 Respostas
- 5516 Exibições
- Última mensagem por adauto martins

Seg Abr 23, 2018 17:52
Funções
-
- conjunto dos números reais
por jose henrique » Sex Set 03, 2010 21:58
- 1 Respostas
- 2134 Exibições
- Última mensagem por MarceloFantini

Sáb Set 04, 2010 13:05
Álgebra Elementar
-
- EQUAÇÕES NO CONJUNTO DOS REAIS
por jose henrique » Seg Set 06, 2010 22:24
- 1 Respostas
- 1768 Exibições
- Última mensagem por Douglasm

Seg Set 06, 2010 23:15
Álgebra Elementar
-
- conjunto de numeros reais
por VERONICALIMA » Sex Nov 29, 2013 16:23
- 1 Respostas
- 1690 Exibições
- Última mensagem por DanielFerreira

Ter Fev 11, 2014 16:42
Conjuntos
-
- Conjunto dos números Reais
por CarolineCecy » Sex Abr 14, 2017 03:29
- 0 Respostas
- 2419 Exibições
- Última mensagem por CarolineCecy

Sex Abr 14, 2017 03:29
Conjuntos
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


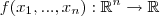 ?
?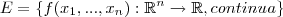
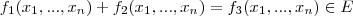
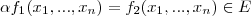

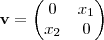 ?
?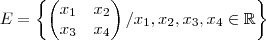
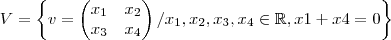
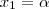 , temos
, temos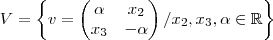 .
. 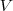 é espaço vetorial então para quaisquer
é espaço vetorial então para quaisquer 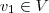 e
e 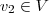 devemos verificar
devemos verificar 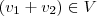 ,
, 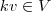 e a existência do elemento neutro.
e a existência do elemento neutro.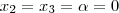 . Ainda,
. Ainda, 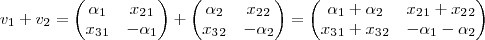
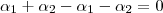 então
então 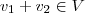 .
.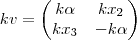
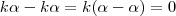 e, portanto,
e, portanto, 





