Olá a todos, estava tentando resolver essa questão que a princípio achei fácil, mas depois de pensar um pouco mais, não cheguei a conclusão final.
O enunciado é:
1) Determinar se o seguinte conjunto é subespaço de R³: W = { (a1,a2,a3) | a1=3a2 e a3=-a2 }
Minha resposta foi:
R = W não é subespaço pois, pela propriedade 2 de subespaço, u + v pertence a W. Já para esse caso:
Dados u,v pertencentes a W => u = ( 3(a2), (a1)/3 , -(a1)/3 ) e v = ( 3(b2) , (b1)/3 , -(b1)/3 ) => u+v = (3(a2+b2) , (a1+b1)/3 , -(a1+b1)/3 ) .
Gostaria de saber, se pelo fato de o sistema não ser determinado, o W não poderia ser subespaço vetorial, pois nesse caso a2 = a1/3 e também a2 = -a3
Agradeço a atenção.


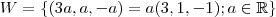 (por simplicidade troquei "a_2 " por "a" ) que é o cojunto de todos os múltiplos de
(por simplicidade troquei "a_2 " por "a" ) que é o cojunto de todos os múltiplos de 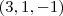 .Afirmamos que
.Afirmamos que  é subespaço do
é subespaço do  .De fato :
.De fato : 
 o vetor nulo do
o vetor nulo do 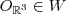 (deixo a cargo de você demonstrar isto)
(deixo a cargo de você demonstrar isto)  Dados
Dados 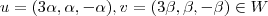 .Temos :
.Temos : ![u+v = (3\alpha + 3\beta , \alpha +\beta , - \alpha - \beta ) = (3(\alpha + \beta) ,\alpha +\beta, -(\alpha + \beta)) =\\ \underbrace{[\alpha + \beta]}_{\in \mathbb{R}}]\cdot (3,1,-1) \in W u+v = (3\alpha + 3\beta , \alpha +\beta , - \alpha - \beta ) = (3(\alpha + \beta) ,\alpha +\beta, -(\alpha + \beta)) =\\ \underbrace{[\alpha + \beta]}_{\in \mathbb{R}}]\cdot (3,1,-1) \in W](/latexrender/pictures/5feea62479765446c0b7bcb1cba9d534.png) .
.  Agora basta mostrar que para todo escalar
Agora basta mostrar que para todo escalar  e vetor
e vetor 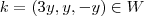 tem-se
tem-se 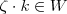 .Tente fazer !!
.Tente fazer !! não exprimir-se de forma única como
não exprimir-se de forma única como  . Pondo
. Pondo 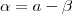 ,para cada escolha arbitrária
,para cada escolha arbitrária  , obtemos um novo número
, obtemos um novo número  que somado a
que somado a 
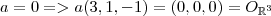
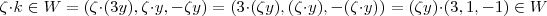 ,
, 
 .
.![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)