Preciso de ajuda nesta questão:
Determinar os autovalores e os autovetores da seguinte treanformação linear:
T :
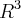

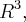 T (x,y,z) = (x+y,y,z)
T (x,y,z) = (x+y,y,z)Minha duvida é: Achei como autovalores 0. 1 e 2, está correto?
não conseguir achar os autovetores associados a esses autovalores pois todos zeravam.
Obrigada.


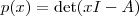 , onde
, onde  é a matriz associada à transformação linear.
é a matriz associada à transformação linear.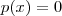 .
.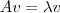 para cada autovalor
para cada autovalor  , ou equivalentemente resolva
, ou equivalentemente resolva 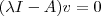 .
.

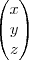 =
= 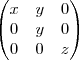
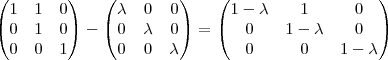
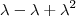 ) ( 1-
) ( 1-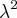 -
- 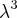
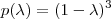 , ou seja, todas as raízes são iguais a um. Agora faça
, ou seja, todas as raízes são iguais a um. Agora faça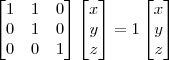 .
.![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)