ESCREVA UM VETOR W COMO COMBINAÇÃO LINEAR DE DOIS VETORES U E V PARA ENCONTRAR OS VALORES DOS ESCALARES A E B, TAIS QUE , W= A.U + B.U. ASSIM, SE FOR POSSÍVEL ESCREVER O VETOR W= (-5,-11) COMO UMA COMBINAÇÃO LINEAR ENTRE U= (3,5) E V= (-1,3), O VALOR DE A + B SERÁ:
A) 2
B) 0
C) 1
D) -1
E) -2
A RESPOSTA CERTA É A LETRA C), MAS COMO POSSO EXPRESSAR ESSE CÁLCULO, POIS ACHO QUE ESTOU FAZENDO ERRADO. EU USEI W=A.U +B.V
(-5,-11) = A(3,5) + B(-1,-3)
(-5,-11) = (3A,5A) + (-B,-3B)
(-5,-11) = (3A,5A - B,-3B)
(-5,-11) = (3A + 5A)
-5= 8A
A= 5/8
(-5,-11) = (-B + (-3B))
(-5,-11)= (-B - 3B)
-11 = -4B
4B = 11
B=11/4
SE EU SOMAR A + B = 23/20 O QUE NÃO CORRESPONDE A NENHUMA DAS ALTERNATIVAS. ONDE ESTOU ERRANDO ?
\\
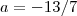
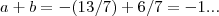
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png "\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}")
![\sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png "\sqrt[]{2}")
e elevar ao quadrado os dois lados)