 por Razoli » Sex Mai 08, 2015 11:25
por Razoli » Sex Mai 08, 2015 11:25
Alguém poderia me ajudar com esse exercicio?
Considere a transformação Linear
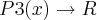
dada por:
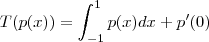
Determine a base do Ker(T) e uma base para a Im(T).
-
Razoli
- Usuário Dedicado

-
- Mensagens: 28
- Registrado em: Sáb Abr 06, 2013 15:42
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Estatistica
- Andamento: cursando
 por adauto martins » Dom Mai 10, 2015 15:43
por adauto martins » Dom Mai 10, 2015 15:43
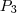
={
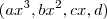
/
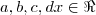
}...
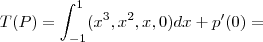
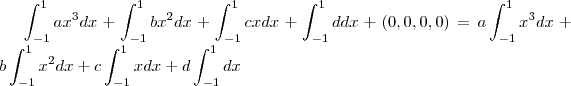
...a integral de funçoes pares em um intervalo simetrico eh 2.
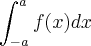
...a integral de funçoes impares em intervalos simetricos eh nula(prove isso)...logo...
![T({P}_{3})=(0+2b.{x}^{3}/3+0+2.dx)[-1,1]=(4/3)b+4d T({P}_{3})=(0+2b.{x}^{3}/3+0+2.dx)[-1,1]=(4/3)b+4d](/latexrender/pictures/f342049ef3527874ae4a6cfb091276b2.png)
...
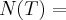
{
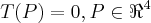
}...logo...
![T(P)=(4/3)b+4d=0\Rightarrow b=-3d\Rightarrow v\in N(T(P))/v=(0,-3d,0,d)=d(0,-3,0,1)\Rightarrow B(N(T))=[(0,-3,0,1)]\in {\Re}^{4} T(P)=(4/3)b+4d=0\Rightarrow b=-3d\Rightarrow v\in N(T(P))/v=(0,-3d,0,d)=d(0,-3,0,1)\Rightarrow B(N(T))=[(0,-3,0,1)]\in {\Re}^{4}](/latexrender/pictures/03b62485f961c07e8af2ed82c63376e3.png)
...
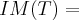
{
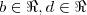
}
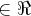
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
Voltar para Álgebra Linear
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Nucleo e imagem
por baianinha » Sex Jan 21, 2011 21:00
- 1 Respostas
- 14736 Exibições
- Última mensagem por LuizAquino

Sáb Jan 22, 2011 11:44
Matrizes e Determinantes
-
- Encontre núcleo e imagem
por carlex28 » Seg Abr 22, 2013 10:10
- 0 Respostas
- 1244 Exibições
- Última mensagem por carlex28

Seg Abr 22, 2013 10:10
Álgebra Linear
-
- [Álgebra Linear] Núcleo e Imagem
por RafaelPereira » Seg Mar 04, 2013 15:39
- 0 Respostas
- 1601 Exibições
- Última mensagem por RafaelPereira

Seg Mar 04, 2013 15:39
Álgebra Linear
-
- [Transformação Linear] Nucleo e Imagem, ache a transformaçao
por vualas » Qua Nov 07, 2012 00:37
- 2 Respostas
- 4256 Exibições
- Última mensagem por adauto martins

Qui Dez 15, 2016 11:12
Álgebra Linear
-
- Nucleo, a sua dimensão e uma base de transformações lineares
por Dethe » Seg Jan 17, 2011 14:15
- 1 Respostas
- 3079 Exibições
- Última mensagem por Renato_RJ

Seg Jan 17, 2011 22:48
Matrizes e Determinantes
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 10:38
Olá ! Tenho essa dúvida e não consigo montar o problema para resolução:
Qual é o racional não nulo cujo o quadrado é igual à sua terça parte ?
Grata.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 12:27

Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 12:55
também pensei que fosse assim, mas a resposta é

.
Obrigada Fantini.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 13:01

Como

:

O que você fez?
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 16:17
eu só consegui fazer a igualdade, não consegui desenvolver o restante, não pensei em fatoração, mas agora entendi o que vc fez.
Obrigada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
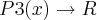 dada por:
dada por: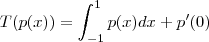

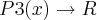 dada por:
dada por: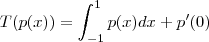

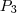 ={
={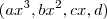 /
/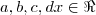 }...
}...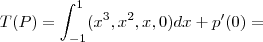
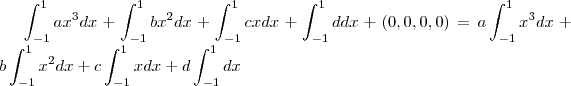 ...a integral de funçoes pares em um intervalo simetrico eh 2.
...a integral de funçoes pares em um intervalo simetrico eh 2.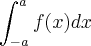 ...a integral de funçoes impares em intervalos simetricos eh nula(prove isso)...logo...
...a integral de funçoes impares em intervalos simetricos eh nula(prove isso)...logo...![T({P}_{3})=(0+2b.{x}^{3}/3+0+2.dx)[-1,1]=(4/3)b+4d T({P}_{3})=(0+2b.{x}^{3}/3+0+2.dx)[-1,1]=(4/3)b+4d](/latexrender/pictures/f342049ef3527874ae4a6cfb091276b2.png) ...
...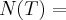 {
{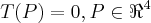 }...logo...
}...logo...![T(P)=(4/3)b+4d=0\Rightarrow b=-3d\Rightarrow v\in N(T(P))/v=(0,-3d,0,d)=d(0,-3,0,1)\Rightarrow B(N(T))=[(0,-3,0,1)]\in {\Re}^{4} T(P)=(4/3)b+4d=0\Rightarrow b=-3d\Rightarrow v\in N(T(P))/v=(0,-3d,0,d)=d(0,-3,0,1)\Rightarrow B(N(T))=[(0,-3,0,1)]\in {\Re}^{4}](/latexrender/pictures/03b62485f961c07e8af2ed82c63376e3.png) ...
...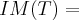 {
{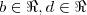 }
} 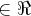


 .
.
 :
: