


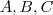 (não colineares ) pertencendo a um plano
(não colineares ) pertencendo a um plano 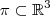 .
.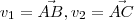 e ambos são paralelos a
e ambos são paralelos a  .
. 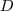 um ponto qualquer deste plano [/tex] . Construímos o vetor
um ponto qualquer deste plano [/tex] . Construímos o vetor 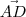 , vemos que
, vemos que 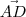 se exprimir como soma de dois vetores , um paralelo a
se exprimir como soma de dois vetores , um paralelo a 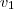 e o outro a
e o outro a  . Ou seja é ,
. Ou seja é ,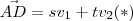 para
para 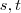 escalares .
escalares .  possui solução , então A,B,C,D estão em um mesmo plano . Caso contrário não .
possui solução , então A,B,C,D estão em um mesmo plano . Caso contrário não . , resulta que os vetores três vetores são L.D .
, resulta que os vetores três vetores são L.D . 
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.