Olá, pessoal.
Estou com dificuldade para isolar o X em uma questão.
(B.A^t)^t.X.B.A^t = 4A.A^t + C.X.B.A^t
O professor isolou o x e ficou assim. Não entendi de que modo ele chegou a isso:
X = [(B.A^t)^t - C]^-1 . 4A.A^t . (B.A^t)^-1
Alguém poderia me explicar, detalhadamente?
Obrigado.
Obs.: o " ^t " significa matriz transposta.


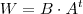 e escrever a eq.matricial como
e escrever a eq.matricial como 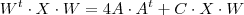
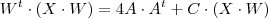
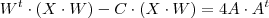
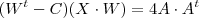 (Se aplicar a distributiva chegará na mesma eq. acima)
(Se aplicar a distributiva chegará na mesma eq. acima)  , a matriz
, a matriz 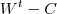 e
e  devem ser invertíveis . Daí é só multiplicar ambos os membros por
devem ser invertíveis . Daí é só multiplicar ambos os membros por 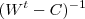 (pela esquerda) e
(pela esquerda) e 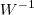 (pela direita) .
(pela direita) . 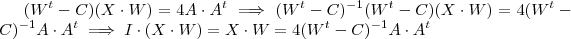 . Agora é só fazer a segunda etapa e dps subst. W por B \cdot A^t .
. Agora é só fazer a segunda etapa e dps subst. W por B \cdot A^t .
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)