 por TLWeber » Dom Out 06, 2013 17:41
por TLWeber » Dom Out 06, 2013 17:41
ola, não lembro mais como resolver o exercico abaixo, gostaria que alguem me desse umas dicas de como resolver o exercicio
determinar a equação geral do plano
perpendicular à reta
r: { x=2+2t
y=1-3t
z=4t
e que contenha o ponto A(-1,2-3)
-
TLWeber
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Dom Set 22, 2013 23:15
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por e8group » Dom Out 06, 2013 21:42
por e8group » Dom Out 06, 2013 21:42
Lembre-se que um plano que passa pelo ponto
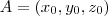
tem possui eq.
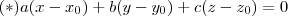
, onde
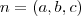
= vetor normal ao plano .
Quanto ao exercício , chamamos de

o plano perpendicular à reta

(dada) e
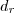
seu vetor diretor.Ora,
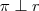
implica
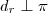
,logo
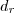
é um vetor normal ao plano

, como foi dado o ponto o qual o plano passa ,basta substituir em (*) .
Agora tente concluir .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Álgebra Linear
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Equações de plano] encontrar a equação de um plano
por GHT1810 » Ter Jul 03, 2018 19:42
- 0 Respostas
- 5367 Exibições
- Última mensagem por GHT1810

Ter Jul 03, 2018 19:42
Geometria Analítica
-
- [´PLANO] Ponto de intersecção de reta com plano
por manuel_pato1 » Ter Set 25, 2012 09:48
- 1 Respostas
- 14966 Exibições
- Última mensagem por LuizAquino

Ter Set 25, 2012 12:11
Geometria Analítica
-
- [Equação do Plano Tangente - Plano Paralalelo]
por raimundoocjr » Qui Out 24, 2013 22:10
- 0 Respostas
- 2945 Exibições
- Última mensagem por raimundoocjr

Qui Out 24, 2013 22:10
Cálculo: Limites, Derivadas e Integrais
-
- Plano
por Rhyu » Dom Abr 08, 2012 10:57
- 2 Respostas
- 1999 Exibições
- Última mensagem por MarceloFantini

Seg Abr 09, 2012 03:40
Geometria Analítica
-
- Plano
por Claudin » Sex Jul 06, 2012 12:32
- 2 Respostas
- 1817 Exibições
- Última mensagem por Claudin

Sex Jul 06, 2012 16:23
Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


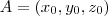 tem possui eq.
tem possui eq. 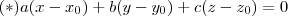 , onde
, onde 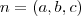 = vetor normal ao plano .
= vetor normal ao plano . o plano perpendicular à reta
o plano perpendicular à reta  (dada) e
(dada) e 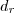 seu vetor diretor.Ora,
seu vetor diretor.Ora, 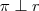 implica
implica 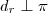 ,logo
,logo 

 .
.



