[Algebra linear e geometria analitica] Duvida

[lucasdemirand]

Olá pessoal, estou com uma duvida no seguinte exercicio, agradeço quem puder me ajudar.
Ache o vetor u, tal que |u|=3?3 e u é ortogonal ao vetor v(2,3,-1) e ao vetor w(2,-4,6). Qual dos vetores encontrados forma ângulo agudo com o vetor j(0,1,0)

[e8group]

Boa noite .Todo vetor não nulo é escrito como 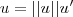onde 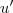é o vetor unitário .Neste caso estamos trabalhando no 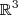,então seja 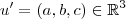tal que 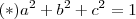.Observe que a ortogonalidade mútua entre os vetores 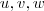implicará um sistema linear homogêneo de duas equações para três incógnitas proveniente do produto interno 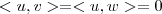.Por outro lado podemos substituir os resultados obtidos no sistema acima e substituir-lós em que nos fornecerá duas respostas distintas(porém iguais em módulo) para uma das variáveis (a,b ou c ) .Após está etapa vamos obter duas resposta possiveis para o exercício satisfazendo a norma de u dada e 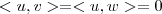.Vemos então que os dois vetores obtidos possuem mesma direção e módulo porém sentidos opostos .Sendo assim ,para determinar o sentido de basta utilizar a seguinte informação "Qual dos vetores encontrados forma ângulo agudo com o vetor j(0,1,0) " .

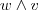Alternativamente ,se você possui um pouco de conhecimento sobre o produto vetorial .Sabemos que o vetor é simultaneamente ortogonal a e a 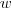.Logo , os vetores e 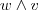são paralelos e portanto um é múltiplo escalar do outro .Assim ,existe um escalar 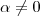tal que , 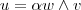.Ora , como 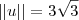,então só pode ser 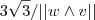ou 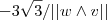.Mas , o ângulo entre os vetores 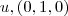é agudo .Seja 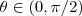o ângulo entre os vetores acima .Como 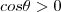concluímos 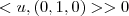, logo ...


Tente concluir .