- CONSIDERE O ESPAÇO VETORIAL MATn (R) COM AS OPERAÇÕES USUAIS, VERIFIQUE SE A FUNÇÃO <A,B> =
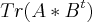 DEFINE UM PRODUTO INTERNO :
DEFINE UM PRODUTO INTERNO :Segundo o professor é necessário testar as 4 propriedades do produto interno.
Eu fiz a primeira já ( Posivitiva Definida: para todo v
 V, <v,v>
V, <v,v>  0, se e somente se v=0v
0, se e somente se v=0v* eu sei que ta um pouco complexo de entender isso, não me familizarei muito com o editor de formulas ainda)
pois bem, não consegui provar as outras 3 propriedades, se alguem puder me ajudar
propriedade 2: SIMETRICA : Para quaisquer v,u
 V, <v,u> = <u,v>
V, <v,u> = <u,v>propriedade 3: ADITIVIDADE: para quaisquer v,u,w
 V, <v+u,w> = <v,w> + <u,w>
V, <v+u,w> = <v,w> + <u,w>propriedade 4: HOMOGENEIDADE: para quaisquer v,u
 V, e para todo k
V, e para todo k  R, <kv,u> = k<v,u>
R, <kv,u> = k<v,u>Se alguem puder ajudar ficarei muito agradecido


![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)