-> Determine o núcleo e a imagem das seguinte transformação linear:
T: C²
 R² dada por T (x+yi , z+ti) = (x+2z , -x+2t)
R² dada por T (x+yi , z+ti) = (x+2z , -x+2t)
 R² dada por T (x+yi , z+ti) = (x+2z , -x+2t)
R² dada por T (x+yi , z+ti) = (x+2z , -x+2t)
 , então
, então  . Resolva o sistema.
. Resolva o sistema.

MarceloFantini escreveu:Para encontrar o núcleo, faça, então
. Resolva o sistema.

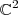 da forma
da forma 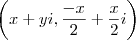 levam a transformação no zero. É só escrever isso.
levam a transformação no zero. É só escrever isso.


Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante