( ) dados um vetor a = 0, sempre existe x E R( x pertencente ao números reais) tal que xa seja um vetor unitário.
(F ) Sejam u, v e w vetores tais que u = v+w logo u, v e w são lados de um triângulo.
creio que esta seja falsa, pois sei que dois vetores podem estar numa mesma reta e portanto não é possível formar um triangulo com apenas uma reta.
( ) se 3u . v = 0 , então u= 0 ou v = 0.
( ) se ||a|| =3, o vetor unitário na direção do vetor -10a é
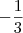 a
a( ) Se a e b são vetores paralelos tais que
 = 2 e
= 2 e  = 4, então a = 2b ou b-2a
= 4, então a = 2b ou b-2aPs me desculpem se abusei do fórum postando 5 perguntas ( já li as regras), como são perguntas estilo " V ou F" creio que seja fácil de responder.
Obrigado.


 , com
, com 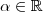 , então
, então  que não é um triângulo.
que não é um triângulo.

 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.