 por Anitojunior1976 » Qui Set 20, 2012 17:39
por Anitojunior1976 » Qui Set 20, 2012 17:39
Qual foi a taxa mensal de desconto comercial utilizada numa operação onde 2 titulos no valor de 5.400,00 e 6.180,00 venciveis respectivamente em 14 e 32 dias foram substituidos por um unico titulo no valor de 11.659,67 vencivel em 28 dias ?
Preciso de uma ajuda com as formulas e montagem do problema .
Grato Junior
-
Anitojunior1976
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Qui Set 20, 2012 15:54
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Curso Tecnico ADM
- Andamento: cursando
 por young_jedi » Qui Set 20, 2012 22:59
por young_jedi » Qui Set 20, 2012 22:59
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por Anitojunior1976 » Sáb Set 22, 2012 19:48
por Anitojunior1976 » Sáb Set 22, 2012 19:48
Olá amigo ele colocou que é juros simples sim e que o resultado é ´4,5% a.m ??? Não consegui entender por favor me ajude
-
Anitojunior1976
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Qui Set 20, 2012 15:54
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Curso Tecnico ADM
- Andamento: cursando
 por DanielFerreira » Sáb Set 22, 2012 22:44
por DanielFerreira » Sáb Set 22, 2012 22:44
Anitojunior1976 escreveu:Qual foi a taxa mensal de desconto comercial utilizada numa operação onde 2 titulos no valor de 5.400,00 e 6.180,00 venciveis respectivamente em 14 e 32 dias foram substituidos por um unico titulo no valor de 11.659,67 vencivel em 28 dias ?
Grato Junior
OPERAÇÃO I:Taxa de desconto (d): ?
Montante (S): R$ 5.400,00
Prazo (n): 14 dias
Desconto (D): ?
Capital (P):
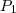
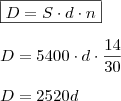
Sabe-se que
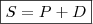
, então:
 OPERAÇÃO II:
OPERAÇÃO II:Taxa de desconto (d): ?
Montante (S): R$ 6.180,00
Prazo (n): 32 dias
Desconto (D): ?
Capital (P):
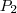
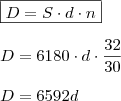
Temos também :
 OPERAÇÃO 'SUBSTITUIDORA':
OPERAÇÃO 'SUBSTITUIDORA':Taxa de desconto (d): ?
Montante (S): R$ 11.659,67
Prazo (n): 28 dias
Desconto (D): ?
Capital (P):

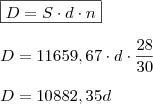
Idem...
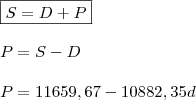
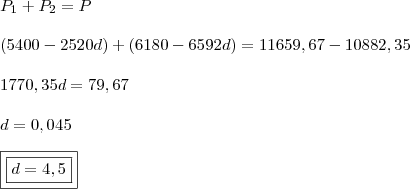
Segue que:
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por young_jedi » Sáb Set 22, 2012 22:45
por young_jedi » Sáb Set 22, 2012 22:45
partindo das tres ultimas equações que eu coloquei
substituindo V1 e V2 na ultima equação temos
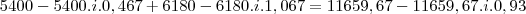
ou seja
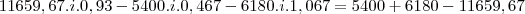
fazendo as multiplicações e as somas
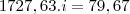
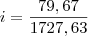
para achar o valor percentual é so multiplicar por 100
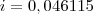
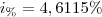
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por Anitojunior1976 » Dom Set 23, 2012 22:45
por Anitojunior1976 » Dom Set 23, 2012 22:45
Olá amigo mais ele não me deu nenhuma dessas formulas que vc postou por isso esotu perdido ok
-
Anitojunior1976
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Qui Set 20, 2012 15:54
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Curso Tecnico ADM
- Andamento: cursando
 por Anitojunior1976 » Seg Set 24, 2012 15:22
por Anitojunior1976 » Seg Set 24, 2012 15:22
Olá amigo ele nunca nem usou estas formulas estou perdido, e ele colocou que tenho que achar o PV de 11,659.67 para fazer o desconto dar nos outros valores poderia colocar a resolução por favor ...
-
Anitojunior1976
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Qui Set 20, 2012 15:54
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Curso Tecnico ADM
- Andamento: cursando
 por young_jedi » Seg Set 24, 2012 16:46
por young_jedi » Seg Set 24, 2012 16:46
PV é o valor presente da sua divida e FV é o valor futuro da sua divida nesse caso
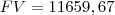
o desconto é calculado pela formula
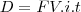
o valor futuro da divida menos o desconto vai dar o valor presente da divida
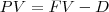
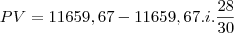
dividi 28 dias por 30 para transformar o tempo em mes.
o i é o valor da taxa que vc quer achar.
como vc não conhece i então PV vai ficar em função de i
voce vai ter que calcular o PV de 5400,00 e o PV de 6180,00
que tambem vão estar em função de i
a soma desses dois PV é igual ao PV 11659,67
fazendo essa igualdade voce vai ter uma equação de i, resolvendo ela voce encontra o valor de i
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
Voltar para Matemática Financeira
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- MATEMÁTICA FINANCEIRA - Equivalência financeira
 por ivolatanza » Ter Fev 28, 2017 15:33
por ivolatanza » Ter Fev 28, 2017 15:33
- 0 Respostas
- 10483 Exibições
- Última mensagem por ivolatanza

Ter Fev 28, 2017 15:33
Matemática Financeira
-
- Matemática Financeira
por plugpc » Sáb Jun 13, 2009 16:58
- 0 Respostas
- 9317 Exibições
- Última mensagem por plugpc

Sáb Jun 13, 2009 16:58
Vestibulares
-
- matematica financeira
por Joziani » Qui Abr 22, 2010 23:18
- 1 Respostas
- 6356 Exibições
- Última mensagem por Molina

Sex Abr 23, 2010 00:07
Matemática Financeira
-
- matematica financeira
por dani chiazza » Ter Mai 18, 2010 15:32
- 1 Respostas
- 4257 Exibições
- Última mensagem por Nino Schnorr

Qua Mai 26, 2010 20:24
Matemática Financeira
-
- Matemática financeira
por Wiviane_1976 » Sex Mai 28, 2010 17:43
- 0 Respostas
- 3293 Exibições
- Última mensagem por Wiviane_1976

Sex Mai 28, 2010 17:43
Matemática Financeira
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.













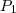
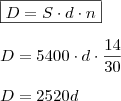
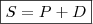 , então:
, então:
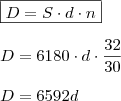


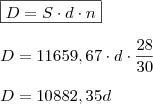
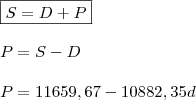


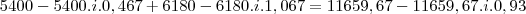
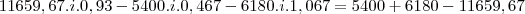
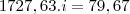
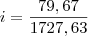
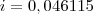
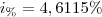
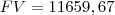
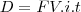
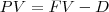
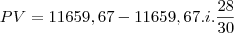


 substitui-se
substitui-se 
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.