 por willwgo » Sex Ago 24, 2012 20:33
por willwgo » Sex Ago 24, 2012 20:33
uma pessoa aplicou cr$ 10.000 a juros compostos de 15 % a.a, pelo praso de 3 anos e 8 meses. admitindo a conversão linear, o montante da aplicação ao final do prazo era de :
A-16.590
B-16.602
c-16.698
d-16.705
e-16.730
obs:
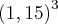
=1,5209
eu tentei passar de ano para mês, mais o resultado nunca da certo o valor q eu achei foi 17.300
se alguem poder me ajudar ...
a resposta certa é a letra E
-
willwgo
- Usuário Dedicado

-
- Mensagens: 33
- Registrado em: Qui Fev 17, 2011 15:59
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por DanielFerreira » Dom Ago 26, 2012 17:16
por DanielFerreira » Dom Ago 26, 2012 17:16
Willwgo,
boa tarde!
P = R$ 10.000,00
i = 15% a.a
n = 3a8m
M = ?
De acordo com o enunciado, como é admitida a conversão linear, não precisamos encontrar a taxa equivalente (Juros Compostos).
Então! Passemos o prazo para anos, assim como a taxa;
3 anos 8 meses =
3 X 12 + 8 =
36 + 8 =
44 meses
Portanto,
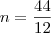
ou

Segue
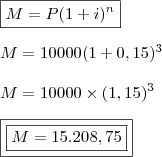 Willwgo
Willwgo,
se fizermos:
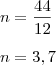
teremos...
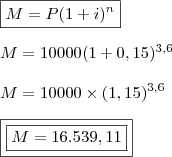
Que passa mais 'perto' do gabarito.
Espero ter ajudado!!
Daniel F.
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
Voltar para Matemática Financeira
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Me ajudem
por geriane » Qui Abr 22, 2010 16:01
- 1 Respostas
- 2840 Exibições
- Última mensagem por Molina

Qui Abr 22, 2010 20:48
Desafios Fáceis
-
- me ajudem ai !!
por weverton » Ter Jun 15, 2010 23:45
- 1 Respostas
- 1644 Exibições
- Última mensagem por Mathmatematica

Qua Jun 16, 2010 01:18
Sistemas de Equações
-
- me ajudem ai!!!
 por weverton » Qui Jul 08, 2010 17:15
por weverton » Qui Jul 08, 2010 17:15
- 2 Respostas
- 8416 Exibições
- Última mensagem por Lucio Carvalho

Qui Jul 08, 2010 19:50
Estatística
-
- me ajudem
por weverton » Qui Out 07, 2010 17:34
- 1 Respostas
- 1667 Exibições
- Última mensagem por MarceloFantini

Qui Out 07, 2010 18:07
Geometria Analítica
-
- me ajudem
por weverton » Seg Nov 08, 2010 16:11
- 7 Respostas
- 3969 Exibições
- Última mensagem por MarceloFantini

Qua Nov 10, 2010 01:43
Logaritmos
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
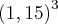 =1,5209
=1,5209
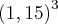 =1,5209
=1,5209
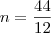 ou
ou 
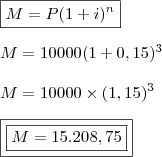
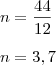
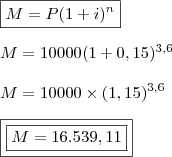



 , avisa que eu resolvo.
, avisa que eu resolvo.

