-
-
Novo APOIA.se AjudaMatemática
por admin em Sáb Abr 25, 2020 19:01
- 0 Tópicos
- 477896 Mensagens
-
Última mensagem por admin

em Sáb Abr 25, 2020 19:01
-
-
Agradecimento aos Colaboradores
por admin em Qui Nov 15, 2018 00:25
- 0 Tópicos
- 529647 Mensagens
-
Última mensagem por admin

em Qui Nov 15, 2018 00:25
-
-
Ativação de Novos Registros
por admin em Qua Nov 14, 2018 11:58
- 0 Tópicos
- 493189 Mensagens
-
Última mensagem por admin

em Qua Nov 14, 2018 11:58
-
-
Regras do Fórum - Leia antes de postar!
por admin em Ter Mar 20, 2012 21:51
- 0 Tópicos
- 699439 Mensagens
-
Última mensagem por admin

em Ter Mar 20, 2012 21:51
-
-
DICA: Escrevendo Fórmulas com LaTeX via BBCode
por admin em Qua Ago 29, 2007 04:04
- 41 Tópicos
- 2110189 Mensagens
-
Última mensagem por Janayna

em Qui Abr 27, 2017 00:04
 por carolmds » Qua Mai 08, 2019 09:12
por carolmds » Qua Mai 08, 2019 09:12
Uma dívida será paga em 24 parcelas semestrais no sistema SAC. Porém, os juros é de 1% ao ano. Para transformar ela ao semestre considero juros simples, 0,5%, ou faço aquela fórmula de taxa equivalente?
-
carolmds
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Ter Mai 07, 2019 19:03
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: economia
- Andamento: cursando
 por Baltuilhe » Seg Mai 13, 2019 02:22
por Baltuilhe » Seg Mai 13, 2019 02:22
Boa noite!
Faça a fórmula de taxa equivalente se a taxa for simplesmente 1% a.a.. Se for 1% a.a. com capitalização semestral, daí só dividir por 2 e obter a equivalente semestral, mesmo.
Portanto:
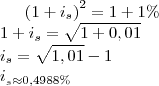
Espero ter ajudado!
-
Baltuilhe
- Usuário Parceiro

-
- Mensagens: 60
- Registrado em: Dom Mar 24, 2013 21:16
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Civil
- Andamento: formado
Voltar para Matemática Financeira
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [juros e taxas equivalentes]questão envolvendo juros p.a
por radfmega » Dom Out 06, 2013 11:12
- 1 Respostas
- 5358 Exibições
- Última mensagem por DanielFerreira

Sáb Nov 01, 2014 19:01
Matemática Financeira
-
- Juros Simples // Juros Compostos
por Roberta » Qui Jul 16, 2009 18:22
- 3 Respostas
- 7382 Exibições
- Última mensagem por Roberta

Qui Jul 16, 2009 19:46
Matemática Financeira
-
- Juros composto valor do juros'
por djeffersound » Qua Jun 23, 2010 19:42
- 0 Respostas
- 3912 Exibições
- Última mensagem por djeffersound

Qua Jun 23, 2010 19:42
Matemática Financeira
-
- --- Juros ---
por rafaasot » Ter Jan 12, 2010 14:06
- 2 Respostas
- 4515 Exibições
- Última mensagem por rafaasot

Qua Jan 13, 2010 10:16
Matemática Financeira
-
- Juros
por Hercilio Matos » Sex Ago 05, 2011 12:27
- 1 Respostas
- 3558 Exibições
- Última mensagem por DanielFerreira

Dom Abr 01, 2012 16:37
Matemática Financeira
Usuários navegando neste fórum: Nenhum usuário registrado e 11 visitantes
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



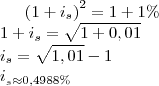

 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
