-
-
Novo APOIA.se AjudaMatemática
por admin em Sáb Abr 25, 2020 19:01
- 0 Tópicos
- 480028 Mensagens
-
Última mensagem por admin

em Sáb Abr 25, 2020 19:01
-
-
Agradecimento aos Colaboradores
por admin em Qui Nov 15, 2018 00:25
- 0 Tópicos
- 537997 Mensagens
-
Última mensagem por admin

em Qui Nov 15, 2018 00:25
-
-
Ativação de Novos Registros
por admin em Qua Nov 14, 2018 11:58
- 0 Tópicos
- 501777 Mensagens
-
Última mensagem por admin

em Qua Nov 14, 2018 11:58
-
-
Regras do Fórum - Leia antes de postar!
por admin em Ter Mar 20, 2012 21:51
- 0 Tópicos
- 722985 Mensagens
-
Última mensagem por admin

em Ter Mar 20, 2012 21:51
-
-
DICA: Escrevendo Fórmulas com LaTeX via BBCode
por admin em Qua Ago 29, 2007 04:04
- 41 Tópicos
- 2156818 Mensagens
-
Última mensagem por Janayna

em Qui Abr 27, 2017 00:04
 por Luan123 » Ter Nov 22, 2016 12:43
por Luan123 » Ter Nov 22, 2016 12:43
Carlos aplicou R$ 8.000,00 durante um mês : Uma parte a taxa de juro simples de 2,4% ao mês, e o restante a taxa de juros simples de 2% ao mês .A parte que ele aplicou a 2,4% ao mês rendeu o dobro de juros do que a parte aplicada a 2% ao mês .Quanto ele recebeu de juros no total?
-
Luan123
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Ter Nov 22, 2016 12:19
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por DanielFerreira » Sáb Nov 26, 2016 18:28
por DanielFerreira » Sáb Nov 26, 2016 18:28
Luan123 escreveu:Carlos aplicou R$ 8.000,00 durante um mês : Uma parte a taxa de juro simples de 2,4% ao mês, e o restante a taxa de juros simples de 2% ao mês .A parte que ele aplicou a 2,4% ao mês rendeu o dobro de juros do que a parte aplicada a 2% ao mês .Quanto ele recebeu de juros no total?
Da parte que Carlos aplicou 2% a.m, temos que:
taxa (i): 2% a.m
juros (J): x
prazo (n): 1 mês
capital (C): c
Daí,
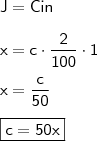
Da parte que Carlos aplicou 2,4% a.m, temos que:
taxa (i): 2,4% a.m
juros (J): 2x
prazo (n): 1 mês
capital (C): 8000 - c
Logo,
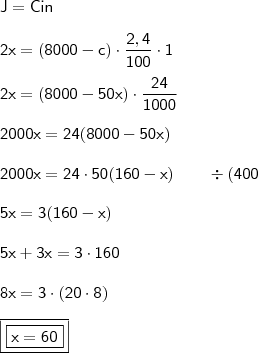
Agora ficou fácil concluir!
Comente qualquer dúvida!
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1728
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Engº Pedreira - Rio de Janeiro
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
Voltar para Matemática Financeira
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Soma total para investimento em juros compostos
por joaodefaria » Ter Set 08, 2009 16:29
- 0 Respostas
- 1421 Exibições
- Última mensagem por joaodefaria

Ter Set 08, 2009 16:29
Matemática Financeira
-
- Questão sobre taxa de juros
por Faborgia » Qui Dez 12, 2013 12:46
- 1 Respostas
- 3347 Exibições
- Última mensagem por DanielFerreira

Ter Fev 11, 2014 15:04
Matemática Financeira
-
- Exercícios sobre Juros Simples
por Lote14 » Sáb Set 26, 2015 10:44
- 4 Respostas
- 17489 Exibições
- Última mensagem por nakagumahissao

Ter Nov 28, 2017 05:53
Matemática Financeira
-
- Exercício da Fundação Carlos Chagas
por Lola » Seg Set 17, 2012 00:02
- 1 Respostas
- 2155 Exibições
- Última mensagem por young_jedi

Seg Set 17, 2012 10:59
Conjuntos
-
- [geometria] funda. Carlos chagas-SP
por my2009 » Qui Fev 04, 2016 11:58
- 2 Respostas
- 5155 Exibições
- Última mensagem por my2009

Ter Fev 09, 2016 10:44
Geometria
Usuários navegando neste fórum: Nenhum usuário registrado e 13 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



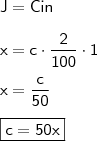
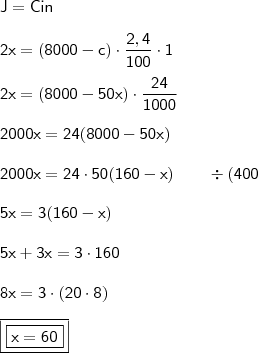

 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.