-
-
Novo APOIA.se AjudaMatemática
por admin em Sáb Abr 25, 2020 19:01
- 0 Tópicos
- 478156 Mensagens
-
Última mensagem por admin

em Sáb Abr 25, 2020 19:01
-
-
Agradecimento aos Colaboradores
por admin em Qui Nov 15, 2018 00:25
- 0 Tópicos
- 531683 Mensagens
-
Última mensagem por admin

em Qui Nov 15, 2018 00:25
-
-
Ativação de Novos Registros
por admin em Qua Nov 14, 2018 11:58
- 0 Tópicos
- 495242 Mensagens
-
Última mensagem por admin

em Qua Nov 14, 2018 11:58
-
-
Regras do Fórum - Leia antes de postar!
por admin em Ter Mar 20, 2012 21:51
- 0 Tópicos
- 705351 Mensagens
-
Última mensagem por admin

em Ter Mar 20, 2012 21:51
-
-
DICA: Escrevendo Fórmulas com LaTeX via BBCode
por admin em Qua Ago 29, 2007 04:04
- 41 Tópicos
- 2120911 Mensagens
-
Última mensagem por Janayna

em Qui Abr 27, 2017 00:04
 por Lulumatematica » Seg Jun 27, 2016 01:25
por Lulumatematica » Seg Jun 27, 2016 01:25
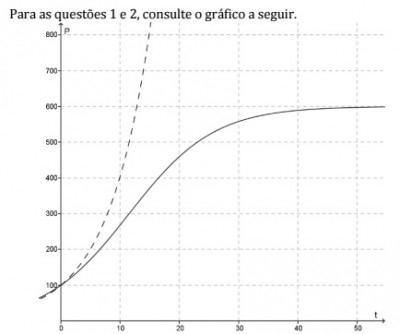
1. Havendo nutrientes suficientes, o crescimento de uma população P de bactérias pode ser modelado em função do tempo t pela equação P(t) = P0(1 + i)^t onde P0 é a população inicial e i é a taxa de crescimento por período. A linha tracejada no gráfico ao lado mostra a função P(t) = 100 ? 1,15^t, que corresponde a uma população inicial de 100 bactérias que aumenta 15% a cada período.
Escolha a alternativa que melhor corresponde à linha tracejada.
a. P cresce de maneira linear até 600, depois não cresce mais. Podemos dizer que limt?? P(t) = 600.
b. P cresce rapidamente no início, e a taxa de crescimento vai diminuindo à medida que a população se aproxima de 600. Dizemos que limt?? P(t) = 600.
c. P cresce sem limitação e de maneira linear. Dizemos que limt?? P(t) = ?.
d. P cresce sem limitação e de maneira exponencial. Podemos dizer que limt?? P(t) = ?.
e. P cresce sem limitação e de maneira exponencial. Podemos dizer que limt?? P(t) = 800.
2. Um modelo um pouco mais realista levaria em conta a capacidade máxima do habitat, representada por K. A equação então fica:
P(t) =K(1 + i)^t/K/P0 + (1 + i)^t -1
A linha cheia no gráfico mostra a função P(t) =600?1,15^t/6+1,15^t?1,ou seja, as mesmas 100 bactérias iniciais crescendo inicialmente a 15% por período, porém agora a capacidade máxima do habitat é 600.
Escolha a alternativa que melhor corresponde à linha cheia.
a. P cresce de maneira linear até 600, depois não cresce mais. Podemos dizer que limt?? P(t) = 600.
b. P cresce rapidamente no início, e a taxa de crescimento vai diminuindo à medida que a população se aproxima de 600. Dizemos que limt?? P(t) = 600.
c. P cresce sem limitação e de maneira linear. Dizemos que limt?? P(t) = ?.
d. P cresce sem limitação e de maneira exponencial. Dizemos que limt?? P(t) = ?.
e. P cresce sem limitação e de maneira exponencial. Dizemos que limt?? P(t) = 800.
3. Geometricamente, a derivada representa
a. os valores de x onde o gráfico da função corta o eixo x.
b. a inclinação da reta tangente ao gráfico da função em um ponto dado.
c. uma parábola.
d. os valores de y onde o gráfico da função corta o eixo y.
e. a soma dos quadrados dos catetos.
- Anexos
-
- grafico
-
Lulumatematica
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Seg Jun 27, 2016 01:01
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Agronomia
- Andamento: cursando
Voltar para Matemática Financeira
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Derivadas] Dificuldade para calcular derivadas CDI 1
por srmai » Seg Nov 04, 2013 01:21
- 0 Respostas
- 1944 Exibições
- Última mensagem por srmai

Seg Nov 04, 2013 01:21
Cálculo: Limites, Derivadas e Integrais
-
- [Derivadas] Interpretação de derivadas e funções
por vinik1 » Qua Out 12, 2011 16:03
- 5 Respostas
- 6818 Exibições
- Última mensagem por vinik1

Qui Out 13, 2011 10:48
Cálculo: Limites, Derivadas e Integrais
-
- [Derivadas] Derivadas em pontos dados
por MarlonMO250 » Sex Mar 01, 2013 21:02
- 6 Respostas
- 4257 Exibições
- Última mensagem por Russman

Sáb Mar 02, 2013 03:42
Cálculo: Limites, Derivadas e Integrais
-
- (derivadas) derivadas com raiz como se faz
por jana garcia » Qua Jun 25, 2014 00:28
- 1 Respostas
- 2448 Exibições
- Última mensagem por e8group

Qua Jun 25, 2014 01:13
Cálculo: Limites, Derivadas e Integrais
-
- [Derivadas] Derivadas com definição de limites
 por concurseironf » Sex Set 05, 2014 18:11
por concurseironf » Sex Set 05, 2014 18:11
- 1 Respostas
- 1700 Exibições
- Última mensagem por DanielFerreira

Dom Set 07, 2014 22:18
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 23 visitantes
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.







