-
-
Novo APOIA.se AjudaMatemática
por admin em Sáb Abr 25, 2020 19:01
- 0 Tópicos
- 479997 Mensagens
-
Última mensagem por admin

em Sáb Abr 25, 2020 19:01
-
-
Agradecimento aos Colaboradores
por admin em Qui Nov 15, 2018 00:25
- 0 Tópicos
- 537819 Mensagens
-
Última mensagem por admin

em Qui Nov 15, 2018 00:25
-
-
Ativação de Novos Registros
por admin em Qua Nov 14, 2018 11:58
- 0 Tópicos
- 501555 Mensagens
-
Última mensagem por admin

em Qua Nov 14, 2018 11:58
-
-
Regras do Fórum - Leia antes de postar!
por admin em Ter Mar 20, 2012 21:51
- 0 Tópicos
- 722447 Mensagens
-
Última mensagem por admin

em Ter Mar 20, 2012 21:51
-
-
DICA: Escrevendo Fórmulas com LaTeX via BBCode
por admin em Qua Ago 29, 2007 04:04
- 41 Tópicos
- 2155875 Mensagens
-
Última mensagem por Janayna

em Qui Abr 27, 2017 00:04
 por leandro moraes » Sáb Out 03, 2015 17:25
por leandro moraes » Sáb Out 03, 2015 17:25
A empresa X possui 60 funcionários, dos quais 15% são
mulheres. De acordo com uma lei aprovada recentemente,
toda empresa do ramo onde atua a empresa X deverá ter,
no mínimo, 40% de mulheres entre seus funcionários.
Para que a empresa X se adapte à nova lei sem demitir
nenhum de seus atuais funcionários e não contratando
novos funcionários homens, ela deverá admitir um número de mulheres, no mínimo, igual a:
a)25
b)22
c)20
d)18
e)15
pessoal, eu achei a letra E como resposta, porém o gabarito diz que é a A???
-
leandro moraes
- Usuário Dedicado

-
- Mensagens: 38
- Registrado em: Ter Jan 12, 2010 23:38
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: contabilidade
- Andamento: formado
 por nakagumahissao » Dom Out 04, 2015 12:17
por nakagumahissao » Dom Out 04, 2015 12:17
No início tínhamos:
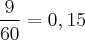
onde 0,15 representa 15%, ou seja:
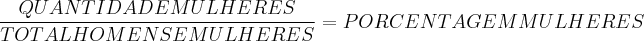
Usando esta mesma idéia, agora com um aumento de mulheres e buscando 40% de mulheres, teremos:
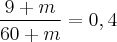
Pois precisamos aumentar o número de mulheres de 9 para 9 + m (m = mulheres) e aumentar também o total na mesma quantidade e desejamos ainda que seja 40% = 0,4. Assim:
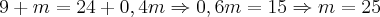
Assim, a resposta seria a letra A.
Eu faço a diferença. E você?
Do Poema: Quanto os professores "fazem"?
De Taylor Mali
-
nakagumahissao
- Colaborador Voluntário

-
- Mensagens: 386
- Registrado em: Qua Abr 04, 2012 14:07
- Localização: Brazil
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Lic. Matemática
- Andamento: cursando
-
Voltar para Matemática Financeira
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Equação de 2°g. Complexa
por Camila Z » Dom Fev 19, 2012 11:04
- 6 Respostas
- 3448 Exibições
- Última mensagem por Camila Z

Dom Fev 19, 2012 23:03
Números Complexos
-
- funçao complexa
por timoteo » Qua Fev 13, 2013 14:22
- 3 Respostas
- 2832 Exibições
- Última mensagem por marinalcd

Ter Mar 05, 2013 13:28
Pedidos de Materiais
-
- Questão de porcentagem
por LuizCarlos » Seg Abr 16, 2012 18:50
- 1 Respostas
- 1403 Exibições
- Última mensagem por DanielFerreira

Qua Abr 18, 2012 22:30
Álgebra Elementar
-
- Formula complexa - ajuda.
por mariosandes » Qui Out 21, 2010 11:24
- 2 Respostas
- 1975 Exibições
- Última mensagem por mariosandes

Sex Out 22, 2010 16:04
Matemática Financeira
-
- equação irracional complexa
por viduani » Sex Jul 13, 2012 20:29
- 1 Respostas
- 2039 Exibições
- Última mensagem por fraol

Sex Jul 13, 2012 21:06
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 13 visitantes
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
zig - Sex Set 23, 2011 13:57
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
Vennom - Sex Set 23, 2011 21:41
zig escreveu:![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Rpz, o negócio é o seguinte:
Quando você tem uma potência negativa, tu deve inverter a base dela. Por exemplo:

Então pense o seguinte: a fração geratriz de 0,05 é

, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
Veja:
![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
A raiz quadrada de vinte, você acha fácil, né?
Espero ter ajudado.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:23
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:24
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


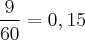
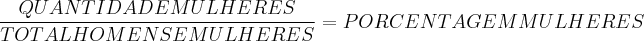
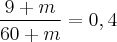
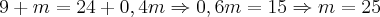

![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.