 por Amandatkm » Qua Mai 08, 2013 20:03
por Amandatkm » Qua Mai 08, 2013 20:03
30. As economias de um clube foram aplicadas por 2 anos e meio com taxa de 2,5% ao mês, no regime
de juros simples. Ao final da aplicação, obteve-se o valor total de R$ 7.350,00. O valor aplicado foi
(A) R$ 4.000,00.
(B) R$ 4.200,00.
(C) R$ 4.400,00.
(D) R$ 4.600,00.
j=cit
7350=c(0,025+30)
7350=0,75c
c=9800 mesmo se eu subtrair 7350 nao da 4200(alternatica certa)
a formula de montante:
m=c(1+0,025+30)
c=236,90(nada a ver)
vejam:
j=4200*0.025*30=3015 subtraindo 7350 da 4200 como eu acho esse 3015 pra achar esse 4200 meu pai?
pireei'
-
Amandatkm
- Usuário Parceiro

-
- Mensagens: 67
- Registrado em: Ter Mar 12, 2013 12:51
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: curso técnico em admiistração
- Andamento: cursando
 por brunoiria » Qua Mai 08, 2013 23:18
por brunoiria » Qua Mai 08, 2013 23:18
Ola Amandatkm,
Vamos lá, a taxa de juros é de
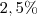
ao mês durante
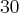
meses, então
a taxa de juros do rendimento será
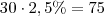
Assim o montante

terá rendimento

no periodo.
A aplicação de rendimento pela equação

Bom vc esqueceu de somar o montante inicial na primeira. e na segunda não é uma soma
A equação para resolver seria

sendo T=total; M=montante, j=Juros, t=Tempo
Espero ter ajudado....
-
brunoiria
- Usuário Ativo

-
- Mensagens: 11
- Registrado em: Sáb Jun 23, 2012 10:32
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Lic Mat
- Andamento: cursando
Voltar para Matemática Financeira
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Pq será que não deu certo?
por Fernanda Lauton » Seg Jul 05, 2010 14:18
- 1 Respostas
- 1534 Exibições
- Última mensagem por Elcioschin

Seg Jul 05, 2010 15:06
Logaritmos
-
- L=R-C - Por favor, fiz certo ou não?
por HamiltonAN » Sex Jun 17, 2011 17:32
- 0 Respostas
- 1422 Exibições
- Última mensagem por HamiltonAN

Sex Jun 17, 2011 17:32
Álgebra Elementar
-
- Estou certo?
por Cleyson007 » Sáb Jun 09, 2012 13:01
- 1 Respostas
- 1547 Exibições
- Última mensagem por Molina

Sáb Jun 09, 2012 14:53
Cálculo: Limites, Derivadas e Integrais
-
- sera que esteja certo
por gramata » Qua Set 02, 2009 17:05
- 1 Respostas
- 1434 Exibições
- Última mensagem por DanielFerreira

Seg Set 28, 2009 10:22
Funções
-
- CONFERIR SE ESTÁ CERTO
por gabimucedola » Sex Abr 02, 2010 18:11
- 1 Respostas
- 1565 Exibições
- Última mensagem por davi_11

Sáb Abr 03, 2010 13:37
Matemática Financeira
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


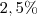 ao mês durante
ao mês durante 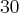 meses, então
meses, então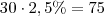
 terá rendimento
terá rendimento  no periodo.
no periodo.
 sendo T=total; M=montante, j=Juros, t=Tempo
sendo T=total; M=montante, j=Juros, t=Tempo

 .
.



