 por Juliane » Sáb Set 04, 2010 17:57
por Juliane » Sáb Set 04, 2010 17:57
Não sei como resolver essa questão e gostaria que alguém me ajudasse:
• Em um certo estado, no mês de julho foi registrada um inflação de 10%, no mês de agosto registrou-se 12% e no mês de setembro 8%. Qual a inflação acumulada nesse trimestre?
No livro tem a resposta, mas não tenho certeza de que está correta: 33,056%
-
Juliane
- Usuário Ativo

-
- Mensagens: 12
- Registrado em: Sáb Set 04, 2010 17:29
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Edificações
- Andamento: cursando
 por MarceloFantini » Sáb Nov 20, 2010 18:36
por MarceloFantini » Sáb Nov 20, 2010 18:36
Suponha um valor
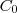
. A inflação após o trimestre será
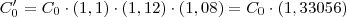
, que é 33,056%.
Ressuscitado pela última vez por Juliane em Sáb Nov 20, 2010 18:36.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Matemática Financeira
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- INFLAÇÃO
por Mandu » Dom Out 24, 2010 15:28
- 1 Respostas
- 1414 Exibições
- Última mensagem por esteban

Sex Out 29, 2010 12:51
Matemática Financeira
-
- inflação
por Abner » Dom Mar 13, 2011 19:00
- 4 Respostas
- 2498 Exibições
- Última mensagem por Abner

Ter Mar 15, 2011 17:01
Matemática Financeira
-
- Inflação
por evarezende » Qui Mai 03, 2012 15:17
- 1 Respostas
- 2461 Exibições
- Última mensagem por Fabiano Vieira

Qui Mai 03, 2012 17:41
Matemática Financeira
-
- Porcentagem e Inflação...
por Willian » Ter Ago 04, 2009 18:02
- 1 Respostas
- 8662 Exibições
- Última mensagem por Felipe Schucman

Ter Ago 04, 2009 23:19
Matemática Financeira
-
- Inflação acumulada
por Catriane Moreira » Dom Nov 07, 2010 17:24
- 1 Respostas
- 2079 Exibições
- Última mensagem por Elcioschin

Dom Nov 07, 2010 22:33
Matemática Financeira
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


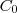 . A inflação após o trimestre será
. A inflação após o trimestre será 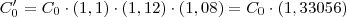 , que é 33,056%.
, que é 33,056%.


 .
.



