Ajuda com fórmulas de crescimento econômico

[RChaves]

Olá, sou parte de uma equipe que está desenvolvendo um jogo no qual você é o prefeito de uma cidade e pode fazer a cidade se expandir. O jogo funciona da seguinte maneira, você manda construir algo e um tempo depois fica pronto, por exemplo, você manda construir um banco, e aí 3 horas depois ele ficará pronto, mas você não precisa esperar 3 horas, você pode mandar construir, fechar o jogo e desligar o computador, aí se você voltar 3 depois, a construção do banco estará concluída. O problema é que existem no jogo várias estatísticas na sua cidade: saúde, alimentação, crescimento populacional, etc.
Por hora, estou com um problema com a parte de economia: o jogador poderá ver numa lista:
A taxa econômica da cidade, que vai de 0% a 100%;
A quantidade de verba ganha por dia, que será calculada através dessa fórmula:
;
A população atual da cidade e a taxa de crescimento populacional

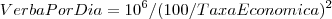Por enquanto não preciso de uma fórmula para calcular o crescimento populacional. O problema que estou tendo é este:
Imaginem uma linha do tempo, começando na última vez que o jogador jogou o jogo e acabando quando ele acabou de abrir o jogo novamente, vamos supor que ele ficou 2 dias sem jogar:

Dia 0 Dia 2

|-------------------------------------------------------------->

Mas nesse tempo, mesmo ele fora do jogo, a população cresceu, vamos supor que de 10 mil habitantes ela passou para 11 mil

10 mil hab. 11 mil hab.

|-------------------------------------------------------------->

Então eu preciso de uma fórmula que calcule o quanto de dinheiro o jogador ganhou nesses dois dias, mas para isso eu preciso de uma fórmula que calcule a taxa econômica da cidade desses dois dias levando em conta:
O nível do banco da cidade, que vai de 1 a 25
A população na cidade, levando em conta se ela variou também
Mas veja bem, a população mínima do jogo é 0 e a máxima 6 milhões, se você tiver 6 milhões de habitantes, sua taxa econômica só será 100% se o nível do banco for 25. Outra coisa, e mais importante, nesses 2 dias, a população cresceu de 10 mil pra 11 mil, uma cidade que teve esse crescimento, obviamente ao final desses dois dias deverá ganhar mais dinheiro do que uma cidade que passou os dois dias com 10 mil habitantes, sem crescimento; porém menos do que uma que já estava com 11 mil, e permaneceu com 11 mil.

Bom, bem complicado, pelo menos pra mim é demais, quebrei muito a cabeça e não consigo encontrar fórmulas adequadas. Por favor, se alguém pudesse me ajudar ficaria muito grato, com certeza terá os devidos créditos no jogo.
Obrigado